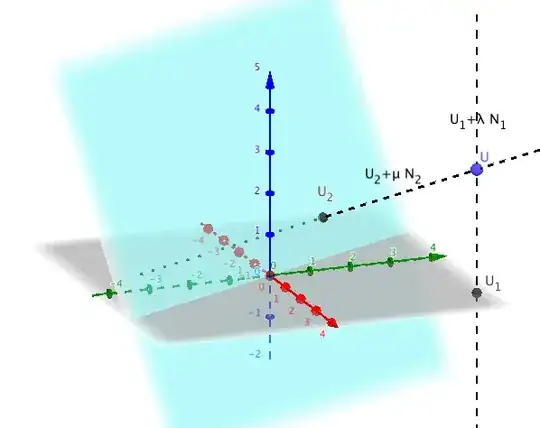
I had recently asked a question regarding getting a 3D vector from 2D projections of it onto two different planes here. After I managed to follow the reasoning behind the first explanation (finding the intersection of scaled normal vectors origination from the two projections in the planes), I was left with seemingly trivial next step of obtaining the coordinates of $\mathbf{U}_{2} =(u_{2},v_{2})$ in terms of the other plane (I include the image created by amd in the answer to the previous question).
The planes I am looking at are from experimental volume data from 2D planes and each 2D plane contained motion information in terms of vectors originating from a point. The same volume was sampled at a different rotation and translation, all of which I know from registering (aligning) the same volume from different measurements. It was rotated/translated using static "base" coordinates.
It seemed to me that I can simply use my $\mathbf{R}_{x}$,$\mathbf{R}_{y}$,$\mathbf{R}_{z}$ rotation matrices I used to align my volume data, but having dabbled with Tait-Bryan angles when I was attempting to solve this via directional cosines, I am not unsure if this naive approach might work. It might have been due to experimental errors, but having tried all 6 directional cosine matrices (from Trait-Bryan angles) I was never able to get a consistent answer.
TL;DR
We have measured values of two 2D vectors $\mathbf{U}_{1} = (u_{1},v_{1})$ and $\mathbf{U}_{2} = (u_{2},v_{2})$, which are projections of some unknown 3D vector $\mathbf{U} = (u,v,w)$. These vectors can be assumed to have a common origin after translating one data volume with the other. We also know the rotations of one data volume to match to the other. If we want to write an equation of the plane B in the coordinate system of plane A, can we simply use the volume rotation angles in the same sequence to transform the basis?
Update 1 In response to amd's comment regarding specific example.
Apologies for slow response - I spent some time double checking the volume registration (to make sure rotation/translation is correct).
It seemed to me that I should be able to solve the above problem in the way amd the describe, but also by doing it numerically via the below change of basis, following explanation on wikpedia: $u_{1} = u_{2}\mathbf{e}_1\cdot\mathbf{n}_1 + v_{2}\mathbf{e}_2\cdot\mathbf{n}_1 + w_{2}\mathbf{e}_3\cdot\mathbf{n}_1$,
$v_{1} = u_{2}\mathbf{e}_1\cdot\mathbf{n}_2 + v_{2}\mathbf{e}_2\cdot\mathbf{n}_2 + w_{2}\mathbf{e}_3\cdot\mathbf{n}_2$,
$w_{1} = u_{2}\mathbf{e}_1\cdot\mathbf{n}_3 + v_{2}\mathbf{e}_2\cdot\mathbf{n}_3 + w_{2}\mathbf{e}_3\cdot\mathbf{n}_3$.
I assumed plane A to be that of the standard basis $ \mathbf{e} = ((1,0,0),(0,1,0),(0,0,1))$. To get the basis of plane B, I naively used a rotation matrix created with Euler-Rodriguez formula shown here, which gave me a $3\times3$ matrix of the new basis vectors n.
I tested this basis by firstly by playing with how a $\mathbf{a} = (a_{x},a_{y},a_{z})$ vector would appear in the different basis (new vector $\mathbf{b} = (b_{x},b_{y},b_{z})$, so I could do some sanity checks on the numerical calculation. The test for a $\mathbf{a} = (1,1,1)$ passed well as expected. I then assumed that I have measured $(a_{x},a_{y})$ and $(b_{x},b_{y})$, and ever so slightly perturbed them - the numerical values went haywire. I suppose this might just mean what amd has mentioned in the previous post, that the normals won't intersect anymore.
My main hesitation to use amd's suggestion was lack of clarity if I can use my volume registration angles, along with 3 rotation matrices in a row, to change from one basis to another. While the test case seemed to suggest that it's fine, perhaps somehow I managed to end up with the right answers, using the wrong approach. (A small note: I suppose strictly speaking my data would be $(z,x,y)$ rather than $(x,y,z)$, but I ignore this for now (partly because I think that this is arbitrarily defined, partly because the angles rotating "around" $y,z$ are small and similar).
Using amd's suggestion + their link to this answer on closest approach, I had to express U2 in the coordinate system of U1. To do that I used the above approach and assumed $(u1,v1,0)$ on the left hand side and solved for $(u2',v2',w2')$. For the "normals to the plane", I used the $\mathbf{e}_{3} (= (0,0,1))$, $\mathbf{n}_{3}$, which I expressed in terms of $\mathbf{e}$, normals to their respective planes.
Because I do not have a baseline measurement (impractical in the circumstances), I need to be absolutely sure the transformation I do are indeed correct.
Update 2
Link to ipython notebook with the calculations is here.
Update 3
I found a typo in my code and realized that I was using the wrong normal (where I previously thought that xyz or zyx didn't matter for standard basis). With this correction, as well as a cross-check via a different method solution by ja72 the results started to look a lot more convincing see geogebra plot here, yet I'm still somewhat worried that projecting $\mathbf{U}_{2}$ onto A by simply using the rotations was indeed correct. The problem is that while projecting the new vector V onto A seems to be a good match with $\mathbf{U}_{1}$, it does not match nearly as well with $\mathbf{U}_{2}$, you can see for yourself by looking down the orange or purple normals (of course it's an approximation, so perhaps I'm hoping too much, but would interesting to know your experience about such things). Most importantly, the "closest approach" doesn't look like it's in the correct location. I can dar a line, L2 to F to get a shorter distance than L1 L2!