1

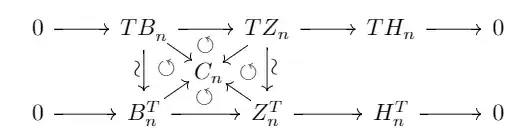
Let $R$ and $A$ be rings, $T:{}_{R}\text{Mod}\rightarrow {}_A\text{Mod}$ be an exact additive functor and $(C_\bullet,d_\bullet)$ a chain complex in ${}_{R}\text{Mod}$. Prove that $$H_n(TC_\bullet,Td_\bullet)\cong TH_n(C_\bullet,d_\bullet) $$

I know this looks too easy, but I can't do an actual proof of this fact.

The thing is that is easy to prove that $T\ker(d_n)\cong \ker(T d_n)$ and $T \ \text{im}(d_{n+1})\cong \text{im}(Td_{n+1})$ but this isomorphims are to abstract so I can't prove that the latter isomorphism is a restriction of the former.

Also, I have the feeling that the additive hypothesis is not needed. Is that correct?

Walter Simon
  • 643
  • I know there is already a question in the site about this. But the solution given there have some problems. For example the equality $F(\partial_{n+1})(F(C_{n+1})))=F(\partial_{n+1}(C_{n+1}))$ is not true without exactness an even with exactness it is just an isomorphism. So you need to show that this isomorphism relates well with respect to the other isomorphism of the kernel. Otherwise is not true the part $$\frac{\ker(F(\partial_n))}{Im(F(\partial_{n+1}))}\stackrel{by (1)(2)}{\cong}\frac{F(\ker(\partial_n))}{F(Im(\partial_{n+1}))}$$. – Walter Simon Oct 11 '17 at 00:10
  • you use additivity in the fact that $T$ maps chain complexes to chain complexes – M. Van Oct 11 '17 at 01:19
  • When we say that a functor preserves the kernel, or the image, of $f:A\rightarrow B$, it means that $T\ker(f)\simeq \ker(Tf)$ as subobjects of $A$. So these isomorphisms relate well with each other (using your words) – Roland Oct 11 '17 at 09:31
  • 1
    $T \ker(d_n)$ is a kernel of $T d_n$. Your issue boils down to how to understand in what way homology is independent of which specific choices of kernels, images, and quotients you use in its construction. –  Oct 11 '17 at 16:18
  • @Roland Thanks for your comments. I think I get a proof of this using the idea of subobject as you suggest. – Walter Simon Oct 11 '17 at 18:21
  • @M.Van where exactly the additivity is needed to prove that? – Walter Simon Oct 11 '17 at 18:22
  • 1
    @WalterSimon we need $Td_i \circ Td_{i-1}=0$, for this we need $T$ to map the $0$ map to the $0$ map and again for this we need additivity. But maybe it follows from exactness as well (?) – M. Van Oct 11 '17 at 18:35
  • Oh right! I completely forgot about that. – Walter Simon Oct 11 '17 at 18:44
  • 2
    @M.Van Yes this follows from exactness. Indeed, an exact functor preserve the zero object, and thus preserve zero maps (these are the maps which factors through the zero object). In fact, an exact functor also preserve direct sums and therefore it will necessarily be additive. – Roland Oct 11 '17 at 20:25

1 Answers1

1

Thanks to the comments I got with a proof that convince me.

As $T$ is left exact is easy to show that $\ker (Td_n)\cong T\ker (d_n)$ as subobjects of $C_n$. Similarly using both right and left exactness one can prove that $\text{im}(Td_{n+1})\cong T \ \text{im}(d_{n+1})$ as subobjects of $C_n$.

Therefore we have the diagram

diagram

Where $B_n=\text{im}(d_{n+1})$, $B_n^T=\text{im}(Td_{n+1})$, and so on

Now using the commutative triangles (given by the isomorphism at the level of subobjects) we can prove that $$(TB_n\rightarrow TZ_n\rightarrow Z_n^T\rightarrow C_n)=(TB_n\rightarrow B_n^T\rightarrow Z_n^T\rightarrow C_n)$$

And then as $Z_n^T\rightarrow C_n$ is a monomorphism the square is commutative. Then we can finish the proof constructing $TH_n\cong H_n^T$ by a diagram chasing or using the universal property of the cokernel.

Walter Simon
  • 643