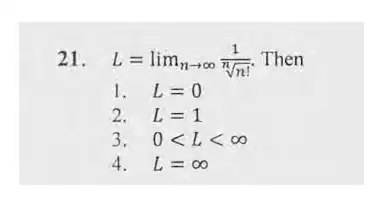0

[CSIR-UGC NET Examination, 2017 June session]

enter image description here

$L=\lim_{n\to \infty}\frac{1}{\sqrt[n]{n!}}$. Then

(1)$L=0$

(2)$L=1$

(3)$0<L<1$

(4) $L=\infty$

Let $x_n=\frac{1}{\sqrt[n]{n!}}$.

Taking logarithm on both sides,

$\log(x_n)=\frac{1}{n}\sum_{k=1} log(\frac{1}{k})$

Using the Cauchy's first theorem on limits,$\lim_{n\to \infty}\log(\frac{1}{n})=-\infty$. So $\lim_{n\to \infty}x_n=0$. Am I correct? Please suggest some short methods. Please note that typing error had occured in the main title. I corrected it. I am apologising for the error.

  • 1
    Isn't it obvious that this is a case of $1/\infty$ ? –  Nov 19 '17 at 11:19
  • @YvesDaoust This result confuses me to apply this, https://math.stackexchange.com/questions/28348/proof-that-lim-n-rightarrow-infty-sqrtnn-1?rq=1 –  Nov 19 '17 at 11:20
  • I didn't think about method given by Find_X.:( –  Nov 19 '17 at 11:22
  • @YvesDaoust His answer is wrong. –  Nov 19 '17 at 11:34
  • 1
    Silently chaging the question is very bad practice. It makes all contributions nonsensical. –  Nov 19 '17 at 11:43
  • I am not aware of "Cauchy's first theorem on limits" by that name but I am aware of the elementary result that if $v_n\to -\infty$ as $n\to \infty$ then $n^{-1}\sum_{j=1}^n v_j\to -\infty$ as $n\to \infty. $.... Another method is that for $2\leq j\in \Bbb N$ we have $\log j>\int_{j-1}^j\log x;dx,$ so for $2\leq n\in \Bbb N$ we have $\log (n!)>\sum_{j=2}^n\int_{j-1}^j\log x;dx=$ $=\int_1^n\log x;dx=$ $n(\log n) -n +1.$ – DanielWainfleet Nov 19 '17 at 12:10

4 Answers4

1

Note that $0\le \dfrac{1}{\sqrt {n!}}\le \dfrac{1}{\sqrt n}$

Since $\dfrac{1}{\sqrt n}\to 0$ as $n\to \infty $ by Squeeze Theorem we have $L=0$

Learnmore
  • 31,062
  • @ManeeshNarayanan; Why did you change the question by editing it?You could have asked a new one.This is not done – Learnmore Nov 19 '17 at 11:37
  • Title has typing error. –  Nov 19 '17 at 11:38
  • Why didn't you read the question completely?. –  Nov 19 '17 at 11:40
  • @ManeeshNarayanan: the editing history clearly shows that you fixed the expression. You should just apologize. –  Nov 19 '17 at 11:46
  • @YvesDaoust. I haven't changed the body of the question. There was error in the title. I was not aggressive.@Find_x If you hurt my comments, I am apologising for that. sorry. –  Nov 19 '17 at 11:57
  • @ManeeshNarayanan; it's okay ;I just felt glad that you realized your fault – Learnmore Nov 19 '17 at 15:17
1

Note that for $x>0$ and $n\in \Bbb N$ we have $e^x = \displaystyle \sum_{n=0}^{\infty}\frac{x^n}{n!} \geq \frac{x^n}{n!}$.

Setting $x=n$, we get $e^n \geq \frac{n^n}{n!}$, hence $e \geq \frac{n}{\sqrt[n]{n!}}$, so $\frac{e}{n} \geq \frac{1}{\sqrt[n]{n!}} \geq 0$, thus $\lim_{n\to \infty}\frac{1}{\sqrt[n]{n!}} = 0$ by the squeeze theorem.

Lukas Heger
  • 20,801
0

Use that if $\lim_{n\to\infty} \frac{a_{n+1}}{a_n}$ exist and $a_n\geq 0$ then $\lim_{n\to\infty} \frac{a_{n+1}}{a_n}=\lim_{n\to\infty} \sqrt[n]{a_n} $. So: \begin{align} \lim_{n\to \infty}\sqrt[n]{\frac{1 } {n! } }=\lim_{n\to \infty}\frac{n!} {(n+1)!}=0 \end{align}

Shashi
  • 8,738
0

Let's try to find $$\lim\limits_{n\rightarrow\infty}(n!)^{\frac{1}{n}}$$

By the Stirling approximation this is equal to

$$\lim\limits_{n\rightarrow\infty}\left(\sqrt{2\pi n}\left(\frac{n}{e}\right)^n\right)^{\frac{1}{n}}=\lim\limits_{n\rightarrow\infty}\left(\sqrt{2\pi n}\right)^{\frac{1}{n}}\left(\frac{n}{e}\right)$$

which obviously diverges. Thus the correct answer is indeed $L=0$

Community
  • 1
user438666
  • 2,040
  • 1
  • 9
  • 23