For all $n \in \mathbb{N_{>0}}$, let $$\phi_{n} = \frac{f_{n+1}}{f_{n}}$$
the ratio between two successive Fibonacci numbers.
I've already shown using Cassini's Identity that $$ \phi_{n} = \phi_{n-1} + (-1)^n \frac{1}{f_{n-1}f_{n}}$$
How do I prove for all $k \in \mathbb{N_{>0}}$ $$\frac{f_{2k}}{f_{2k-1}} = \phi_{2k-1} < \phi_{2k} = \frac{f_{2k+1}}{f_{2k}}$$ and show that the subsequence $\phi_{2k}$ is monotone decreasing, while subsequence $\phi_{2k-1}$ is monotone increasing?
For the first question, move $\frac{f_{2k}}{f_{2k-1}}$ to the right side of the equation and simplify the result, giving $$0\lt\frac{f_{2k+1}f_{2k-1}-(f_{2k})^2}{f_{2k}f_{2k-1}}$$ Then multiply both sides by $f_{2k}f_{2k-1}$. Use Cassini's Identity on the right side. As $1^{2k}$. Therefore, $\phi_{2k-1}\lt\phi_{2k}$ is true. Before going to the second question, I will give some background information. There are 3 ways that an approximation approaches a number. The first way is to increase toward that number. An example is how $\left(1+\frac1n\right)^n$ would approach $e$. The second way is decreasing toward that number. A final way is to alternate between being too high and too low. An example is the Gregory Series, as shown here: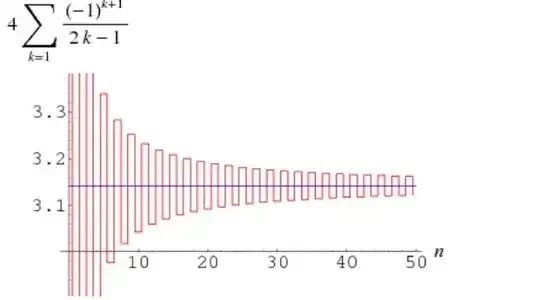 
We can define both functions above as a function and see how this acts. For example, if we call $\left(1+\frac1n\right)^n$ $\Omega(n)$, and $n=1, 3, 5, 7 ,9$ e.t.c. $\Omega (n)$ is increasing, and the same happens when $n=2, 4, 6, 8, 10$ e.t.c.
But in the Gregory series, when $n$ is odd there is an increase and will be above the values next to it(i.e. difference of 1), but when $n$ is even there is a decrease and below the numbers next to it. The process will also occur slower and slower as $n$ increases. This will only stand true for convergent series ($x^2$ is divergent and it will not work for this), but $\phi_x$ converges to \Phi. As $\phi{2k}$ is decreasing but $\phi{2k+1}$ is increasing, they must be fluctuating around /Phi. So all we need to do now is to prove that $\phi_{2k+1}\lt\phi_{2k}$ is true. We move the numbers on the left to the right and multiply, giving us: $$0\lt\frac{-f_{2k+2}f_{2k}+(f_{2k+1})^2}{f_{2k}f_{2k-1}}$$. Multiply both sides by f_{2k}f_{2k-1}. Define $m$ as $2k+1$. Then replace $k$ with $m$, giving us $$0\lt-f_{m+1}f_{m-1}+(f_{m})^2$$ So we now multiply all by -1 and place in brackets, while putting a negative sign in front of the bracket: $$0\lt\left(f_{m+1}f_{m-1}-(f_{m})^2\right)$$. Use Cassini's identity, and as $m$ is odd, we get: $$0\lt-(-1^m)=-(-1)=1$$ This gives $0\lt1$, which must be true. So, $\phi_{2k}$ is decreasing and $\phi_{2k+1}$ is increasing towards $\Phi$.
