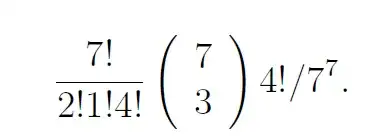Dividing balls into cells probability question

Question

Question: We randomly distribute 7 balls into 7 cells. What is the probability that there are exactly 2 empty cells and there is a cell containing exactly 3 balls?

Answer:

By the answer I understand that the balls are distinct (Omega = 7^7).

I tried to solve it and got to different solution:

Lets define A - There are exactly 2 cells empty B - There is a cell that contains 3 balls

I want to calculate by the formula $P (A \cap B) = P(B|A)P(A)$

I got that $$P(A) = {7 \choose 2}\cdot5!\cdot5\cdot5\cdot{7 \choose 5}/7^7$$

and that $$P(B|A) = \frac{5! \cdot 5 \cdot {7 \choose 5}}{5^7}$$

Therefore $P (A \cap B) = P(B|A)P(A)$ is different from the real result.

Can someone understand why the answer is write? Or maybe where am I missing?

Answer 1

The probability that exactly two urns are empty:

• Pick which two urns are the empty urns in $\binom{7}{2}$ ways
• For the remaining five urns, since none are empty we will have either four with one ball in it and one with three, or we will have three with one ball in it and two with two balls each. Break into cases:

---

• If in the first case, pick which urn received three balls in $5$ ways.

• Finally, pick how to distribute the balls into the urns so that each gets their respective total, for example by picking first which three balls go into the urn needing three balls and then pick which ball goes into the left-most urn which should get one ball, etc... this can be done in $\binom{7}{3}4!$ ways.

(As an aside, we could have stopped here for the originally asked problem, as we would have a grand total of $\binom{7}{2}\cdot 5\cdot \binom{7}{3}\cdot 4!$ ways to have exactly two empty bins and one bin with three balls. Dividing by $7^7$ gives the answer given by the book after noting that $\binom{7}{2}5=\frac{7!}{2!1!4!}$)

---

• In the second case, pick which two urns receive two balls each in $\binom{5}{2}$ ways.

• Then, pick which balls go into which urns, starting for example with the left-most urn that receives too balls, eventually totalling $\binom{7}{2}\binom{5}{2}3!$ ways.

Combining this information, we get that $$Pr(A)=\frac{\binom{7}{2}\left(5\binom{7}{3}4!+\binom{5}{2}\binom{7}{2}\binom{5}{2}3!\right)}{7^7}$$

Next, we can attempt to calculate $Pr(B\mid A)$. Unfortunately, I do not see a convenient approach to calculating this without first calculating $Pr(A\cap B)$ directly. In your attempt at calculations, you have a denominator of $5^7$ which would not make sense because within those $5^7$ outcomes, some of those have additional empty urns which should have been ignored as they do not satisfy the hypothesis that there are exactly two empty urns.

Answer 2

1. Premise

The question you are given starts as "We randomly distribute 7 balls into 7 cells"

There is here a subtle point to clearify, as a first step.

"throwing, i.e. sequentially place, (distinguishable/undistinguishable) balls into (d/u) cells"
and
"distributing, (or placing, or arranging) balls (d/u) into (d/u) cells"

would lead to consider different spaces of elementary events (equi-probable events), also depending on the lexical intepretation, and is a frequent source of misunderstanding in this kind of a problems.

See, e.g., this post.

2. The answer you are given

Not knowing the exact interpretation of the question, let's take it backwards and see which intepretation the answer you have been given could correspond to. $$ P = \left( {{{7!} \over {2!1!4!}}} \right)\quad \left( {\left( \matrix{ 7 \cr 3 \cr} \right)4!} \right)\quad {1 \over {7^{\,7} }} $$

Now

The first term $$ {{{7!} \over {2! \; 1! \;4!}}} $$ is the number of ways to align $2$ cells labelled A, $1$ cell labelled B and $4$ cells labelled C.
These correspond to the two empty cells, the one filled with three balls, and the four non-empty (i.e. equally filled with one ball each).
So the cells are distinguished by their position in the line and for their label = content.

The second term $$ \left( \matrix{ 7 \cr 3 \cr} \right)4! = \left( \matrix{ 7 \cr 4 \cr} \right)4! = 7^{\,\underline {\,4\,} } = 7 \cdot 6 \cdot 5 \cdot 4 $$ is the number of ways to place $4$ labelled balls out of a total of $7$, into $4$ distinguishable cells.
The remaining $3$balls go into the only possible cell. However, there is not a $3!$ factor to account for their permutation inside that cell.
That means that the balls' label order inside the cell B is not taken into account, or that it is considered fixed, for instance increasing. Also the ordering inside each cell C (as well as A) can be considered fixed.

Thus the whole picture matches with the process of randomly throwing undistinguishable balls into distinguishable cells, which justifies the division by $7^7$.