Hello,
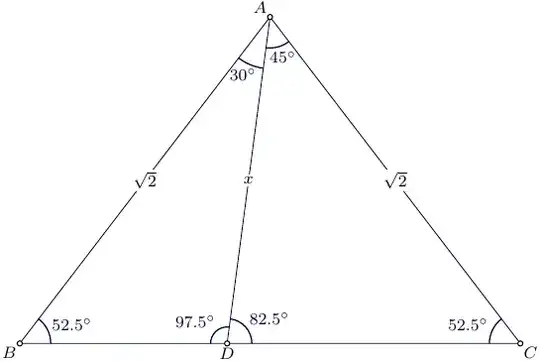
A $\triangle ABC$ has a point $D$ on $BC$ such that $\angle BAD = 30$ and $\angle CAD = 45$. Both $AB$ and $AC$ are of the length $\sqrt{2}$. Find the length of $AD$.
This is what I have done:-
Taking $AD$ as $x$ and $DC$ as $y$, and then using law of cosines for $y$, we get $y^2 = 2 + x^2 - 2x$.
Taking $BD$ as $k$, and applying law of cosines on $k$, we get $k^2 = x^2 + 2 - x*root6$
Taking law of cosines on $k + y$ we get, $(k + y)^2 = 5 - root3 ( cos 75 = root3 - 1/ 2*root2)$
And now I'm stuck at this step. I have no idea on how to go forward after this step.
ANY HELP IS APPRECIATED(if possible in trigonometry plz).
This is not a part of the question but can someone give me a link for the quick reference of mathjax editing?