6

Given sets $A=\{1,2,\dots ,10\}, B=\{1,2,\dots,12\}$. Let $S\subset A\times B$ s.t. $|S|=61$.

Prove that there exist three pairs $(x_1,y_1),(x_2,y_2),(x_3,y_3)$ in $S$ which fulfill:$$ x_1=x_2,\quad |y_1-y_2|=1,\quad |x_2-x_3|=1,\quad y_2=y_3 $$

Progress:
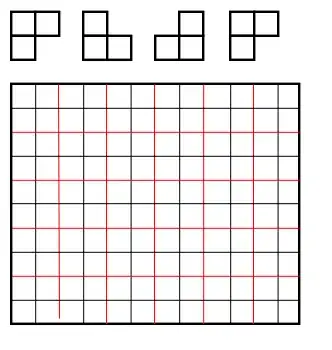
I figured that there are at most $4$ legitimate patterns which a randomly picked pair (e.g $(a,b)$) can fit into:

$1.$ $(a,b-1),(a,b),(a-1,b)$
$2.$ $(a,b-1),(a,b),(a+1,b)$

$3.$ $(a,b+1),(a,b),(a-1,b)$
$4.$ $(a,b+1),(a,b),(a+1,b)$

If those patterns contribute, I'm struggling to define proper sets which relate to them in order to apply the pigeonhole principle.

Slavik Egorov
  • 523

2 Answers2

6

Let's partition $A\times B$ into $30$ little $2\times 2$ squares : explicitely, we write the disjoint union as follows :

$$ \begin{align} A\times B &= \bigcup_{a=1}^5\bigcup_{b=1}^6 \{(2a-1,2b-1),(2a-1,2b),(2a,2b-1),(2a,2b)\} \\ &=: \bigcup_{a=1}^5\bigcup_{b=1}^6 X_{a,b}. \end{align} $$

By the pigeonhole principle, there is a square $X_{a,b}$ that contains at least $3$ elements of $S$ (if it was not the case, $\lvert S \rvert$ would be less than $2\times 30=60$).

Now among those $3$ elements, apply again the pigeonhole principle : two of them must have the same $x$-coordinate. These two will be $(x_1,y_1)$ and $(x_2,y_2)$, and the third element of $S$ inside the square is $(x_3,y_3)$.

tristan
  • 2,883
4

enter image description here

We are trying to avoid one of the four pieces above. Consider the $30$ red $2$ by $2$ squares, each of these can have at most two squares filled in.

Donald Splutterwit
  • 36,613
  • 2
  • 26
  • 73