5

I would like to diagonalise a matrix $M$ of the form

$$ M = \left(\begin{matrix} M_{11}&\ldots&M_{1n}\\ \vdots&\ddots&\vdots\\ M_{n1}&\ldots&M_{nn} \end{matrix}\right), $$ where each element $M_{ij}$ is a square diagonal matrix itself and, in general, $M_{ij}\neq M_{ji}$, i.e. $M$ is not symmetric.

Of course, I can consider $M$ just like any other matrix and diagonalise it numerically, but I am wondering whether the peculiar structure of the matrix would allow for a less brute-force approach.

Here are some first observations from numerical simulations. I generate a matrix by populating the diagonals with standard normal random variables. For three blocks and rank ten for each block we get:

synthetic matrix

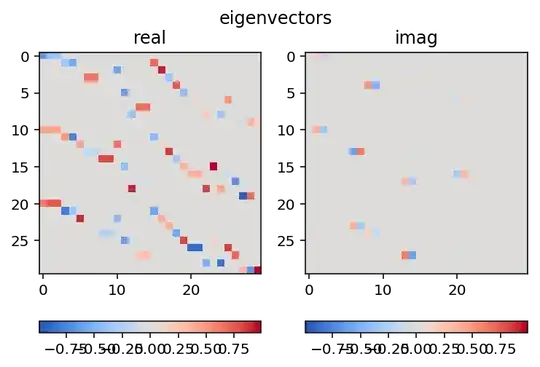
The matrix of eigenvectors shows some structure but none that I can easily interpret:

matrix of eigenvectors

From larger simulations, the number of nonzero real elements of the eigenvector matrix is equal to the number of nonzero elements in $M$, i.e. the number of blocks squared times the rank of each block. The number of nonzero imaginary elements does not appear to be constant for a given block rank and number of blocks, but it is linearly related to the block rank.

Till Hoffmann
  • 755
  • Eigenvectors can be put in any order. I wonder if reordering the columns of the eigenvectors matrix could get anything interesting – Nick Alger Dec 24 '17 at 15:07
  • You can reorder the rows and columns of your matrix to make it block diagonal in the usual sense. These blocks can be independently eigen-analyzed, which must be a cost saving. – kimchi lover Dec 24 '17 at 16:38
  • Can you please tell me how to find the inverse of such a matrix, i e block matrix with diagonal blocks? – Manu S Pillai Sep 22 '21 at 15:26

1 Answers1

3

As noted by kimchi lover, the matrix can be block-diagonalised by reordering the rows and columns. In particular, thinking of the matrix as an adjacency matrix of a graph, there are as many connected components as the size of each block, and the $i^\mathrm{th}$ block comprises of the $i^\mathrm{th}$ elements of all the blocks.

The block-diagonal matrix can be easily diagonalised by diagonalising $p$ matrices of shape $k\times k$, where $k$ is the number of blocks and $p$ is the rank of the original blocks.

Example code is here.

Till Hoffmann
  • 755