0

For, $\int_0^{\infty} \frac{\arctan(x)-\arctan(2x)}x \mathrm dx$

Let, $I_1=\int_0^{\infty} \frac{arctan(x)}x\mathrm dx$ and $I_2=\int_0^{\infty} \frac{\arctan(2x)}x\mathrm dx$

For, $I_1$ let $x=\frac 1u $ so $I_1=\int_{\infty}^{0} \frac{\arctan(\frac1u)}{\frac1u}\left(-\frac1{u^2}\right)\mathrm du$ $=\int_0^{\infty} \frac{arccot(u)}{u}du$

From which it follows, $I_1=\int_0^{\infty} \frac{\frac\pi2-\arctan(x)}x\mathrm dx$ So, $2I_1=\int_0^{\infty} \frac{\frac \pi2}x\mathrm dx$

In the same way it can be shown that, $2I_2=\int_0^{\infty} \frac{\frac\pi2}x\mathrm dx$

So, $2I=2I_1-2I_2=0$

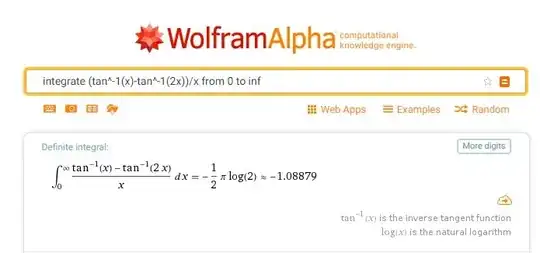
But, Wolfram Alpha says, enter image description here

So, where is my error?

Martin Sleziak
  • 53,687
Partha Sarker
  • 547

4 Answers4

10

Consider the following erroneous computation:

\begin{align*} \log 2 &=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots\\ &=\left(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots\right) -2\left(\frac{1}{2}+\frac{1}{4}+\cdots\right)\\ &=0.\end{align*}

This mistake is in spirit the same as what you did in your computation.

Here is one possible computation. Fix $ R > 0$ and introduce

$$ I_1 = I_1(R) = \int_{0}^{R} \frac{\arctan (x)}{x} \, dx, \qquad I_2 = I_2(R) = \int_{0}^{R} \frac{\arctan (2x)}{x} \, dx. $$

Using the substitution $2x \mapsto x$, we have

$$ I_2 = \int_{0}^{2R} \frac{\arctan x}{x} \, dx $$

and hence

$$ I_1 - I_2 = -\int_{R}^{2R} \frac{\arctan x}{x} \, dx \stackrel{(x=Rt)}{=} -\int_{1}^{2} \frac{\arctan(Rt)}{t} \, dt. $$

So taking $R \to \infty$, we have

$$ \int_{0}^{\infty} \frac{\arctan x - \arctan (2x)}{x} \, dx = -\int_{1}^{2} \frac{\pi/2}{x} \, dx = -\frac{\pi}{2}\log 2. $$

(Remark. Of course, interchanging the limit and the integral is in general now allowed. In our case, this is easily justified by the following inequality

$$ \frac{\pi}{2}\arctan(R) \leq \int_{1}^{2} \frac{\arctan(Rt)}{t} \, dt \leq \frac{\pi}{2}\arctan(2R). $$

Applying the squeezing lemma indeed establishes the desired convergence.)

Sangchul Lee
  • 167,468
6

Let's start off with $$\begin{align}I(a)&=\int_0^\infty\dfrac{\arctan x-\arctan ax}x\mathrm dx\\I'(a)&=\int_0^\infty-\dfrac1{1+a^2x^2}\mathrm dx\\&=-\dfrac1a\int_0^\infty\dfrac1{1+u^2}\mathrm du\qquad[\text{Taking }u=ax]\\&=-\dfrac1a\arctan(u)\bigg|_0^\infty\\&=-\dfrac\pi{2a}\end{align}$$ And now, we integrate both sides with respect to $a$

$$\begin{align}I'(a)&=-\dfrac\pi{2a}\\I(a)&=-\dfrac\pi2\ln a+C\end{align}$$ At $a=1,C=0$ So,we can write

$$I(a)=-\dfrac\pi2\ln a$$

And hence,

$$\begin{align}I(2)&=\int_0^\infty\dfrac{\arctan x-\arctan 2x}x\mathrm dx=-\dfrac\pi2\ln 2\end{align}$$

This is what WolframAlpha gives you.

And if you want, just use Frullani's integral which says that $$\int_0^\infty\dfrac{f(ax)-f(bx)}x\mathrm dx=[f(0)-f(\infty)]\ln\left(\dfrac ba\right)$$

Awnon Bhowmik
  • 1,724
5

By Fubini's Theorem, \begin{eqnarray} &&\int_0^{\infty} \frac{\arctan(x)-\arctan(2x)}x \mathrm dx\\ &=&\int_0^{\infty} \int_1^2\frac{1}{1+t^2x^2}\mathrm dt \mathrm dx\\ &=&\int_1^2\int_0^{\infty}\frac{1}{1+t^2x^2}\mathrm dx \mathrm dt\\ &=&\int_1^2\frac{\arctan(tx)}{t}\bigg|_{x=0}^{x=\infty}dt\\ &=&\int_1^2\frac{\pi}{2t}dt\\ &=&\frac{\pi}{2}\ln 2. \end{eqnarray}

xpaul
  • 44,000
1

Not for sure, but when you made $x=1/u$, you cant afirm that $x\to 0$ will $u\to \infty$ (because the negative side) and when substitue for integrating $\displaystyle \int_{\infty}^0 $ thats not a usal think. Maybe, the error is quit up here (our close). Those integrals need a hyred tools, like dilogarithm $\displaystyle \Big( \text{Li}_2(z)=\sum_{n=1}^\infty \dfrac{z^n}{n^2}\Big)$. Try https://www.integral-calculator.com/, they can explain whey better then me.

Gustavo Mezzovilla
  • 763