1

Recently, I have encountered this problem:

"Given three lines in the normal 3-dimensional Euclidean space (with a given regular coordinate system) with equations: $\left\{ \begin{array}[l] .y = 0 \\ z = 0 \end{array} \right.$, $\left\{ \begin{array}[l] .x = y \\ z = 1 \end{array} \right.$ and $\left\{ \begin{array}[l] .x = 0 \\ z = 2 \end{array} \right.$.

Find the ruled quadratic surface which adopts these lines."

As far as I try to find it, I really have no idea how to proceed. Please give me a hint.

Thank you for reading.

Jean Marie
  • 81,803
ElementX
  • 922

1 Answers1

2

(see figure 1 below)

Let us rewrite the 3 line equations under the equivalent form :

$$(L_1) \ \left\{ \begin{array}[ccc] .(2-z)y &=& zx \\ \ \ z& =& 0 \end{array} \right. , \ \ \ \ \ (L_2) \ \left\{ \begin{array}[rcc] .(2-z)y &= &zx \\ \ \ z& =& 1 \end{array} \right., \ \ \ \ \ (L_3) \ \left\{ \begin{array}[rcc] .(2-z)y& =& zx \\ \ \ z &=& 2 \end{array} \right.$$

Let $(S)$ be the 2nd degree surface with equation:

$$\tag{1}(2-z)y = zx$$

For all $k, \ \ (L_k) \ \subset \ (S) $ (see Remark 1). Thus (1) is a solution to your question (it would remain to show that it's unique, but the way your question is formulated, you have to find the existence of a solution but not prove its unicity ; about unicity, see Remark 2).

Equation (1) can be written under the equivalent form $2y = (x+y)z$, or $Z = XY$ with the bijective linear change of variable $$\left\{ \begin{array}[l] .X= x& + &y&\\ Y=& && z \\ Z= & &2y & \end{array} \right.$$ Thus, it is a hyperbolic paraboloid (https://tex.stackexchange.com/q/19921).

Remark 1 : Let us explain the fact that (for example) $(L_2) \subset (S)$ ; it is equivalent to show that the defining properties of $(L_2)$ imply the defining property of $(S)$.

Indeed, $(2-z)y=zx$ and $z=1$ imply that $(2-z)y=zx$... just because $(p \& q) \implies p.$

Remark 2 : There is a general result by Hilbert [that can be found in his book with Cohn-Vossen : "Mathematics and the imagination"] saying that, being given 3 "skew" lines in general position in $\mathbb{R^3}$, there is a unique (ruled) quadric that contains these lines ; it is in general an hyperboloid with one sheet ; exceptionally (as is the case here), it is a hyperbolic paraboloid. See (Equation of a regulus) and as well (Hyperboloids of one sheet, hyperbolic paraboloids, and Hilbert's famous "three skew lines").

Remark 3 : There is a helicoidal surface $(H)$ (https://en.wikipedia.org/wiki/Helicoid) i.e., a spiraling staircase represented in figure 2 containing straight lines $(L_1),(L_2)$ and $(L_3)$. It is very different from surface (S): it's not a second degree surface : for example, a vertical line passing through $(H)$ intersects it an infinite number of times instead of at most twice for $(S)$. The visible difference between $(S)$ and $(H)$ is that the rotation pace is not uniform for lines on $(S)$: it is maximum for $z=1$ and slows down and tends to zero when $z \to \infty$.

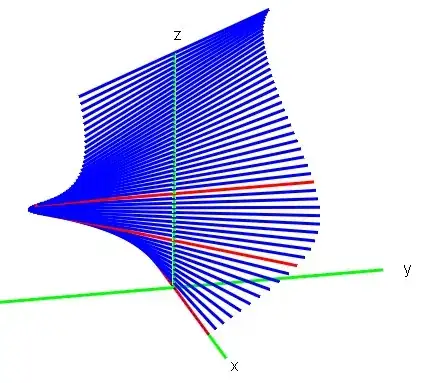
enter image description here

Fig. 1 : Hyperbolic paraboloid (S). $z$ varies from $0$ to $5$. In red: the given lines $(L_k)$.

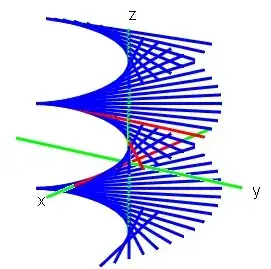
enter image description here

Fig. 2 : Helicoid $(H)$ that is a ruled surface containing the $(L_k)$ but is not a solution to the question because it is not a quadric surface (with second degree equation).

Jean Marie
  • 81,803
  • @achille hui Thanks. About the question of (ruled) quadrics uniquely defined by three pairs of lines, have you seen this interesting recent question: (https://math.stackexchange.com/q/2543857) which has received no answer ? – Jean Marie Dec 29 '17 at 15:53
  • Haven't seen that question. I know how to find the equation of the ruled surface but don't know how to prove it is unique. I'll probably order Hibert and Vossen's book from Amazon. – achille hui Dec 30 '17 at 04:57
  • Thank you, sir.

    Your solution is indeed an elegant one. However, I can't figure out how you got the idea of representing the three given lines like you did. Is there a general way to find out the representation, or you just simply figure out the surface by your experience?

     – ElementX Dec 30 '17 at 07:01
  • Good question. I first draw a figure and saw what I called the rotating effect, with a projection on the xOy that was always of the form $y=ax$ but I knew that $a$ should be function of $z$. $a$ couldnt be a linear function of $z$ (otherwise, we would have an helicoid). And it should be at most of the form $a=(pz+q)/(rz+s)$ for complying with a second degree equation. Observing the equations, I realized that $a=z/(2-z)$ was a good solution. Yes, a part of my reasoning came from my experience... – Jean Marie Dec 30 '17 at 07:15
  • I see, sir. If the given lines have "uglier" equations (general cases), is there still a way to get the desired surface? According to what I read from sir achille hui's reference, there is always a quadratic ruled surface through 3 given skew lines. Is there a guaranteed technique now? Thank you. – ElementX Dec 30 '17 at 10:06
  • Yes, there is a guaranteed technique that is outlined in the first reference I give in my Remark 2 : it is based on projective geometry. Maybe the way it is written ( though very neat ) can be puzzling. A different approach, still using projective geometry, could be to map the 3 lines onto a standard $(H_1)$ (one-sheeted hyperboloid) with equation $x^2+y^2=z^2+1$ by a projective transform. – Jean Marie Dec 30 '17 at 10:39