Why can we maximize $\frac{k-1}{n}(\mathrm{H}_{n-1}-\mathrm{H}_{k-2})$ for $2\leq k\leq n-1$ by substituting $\mathrm{H}_l$ with $\ln(l)$?

Question

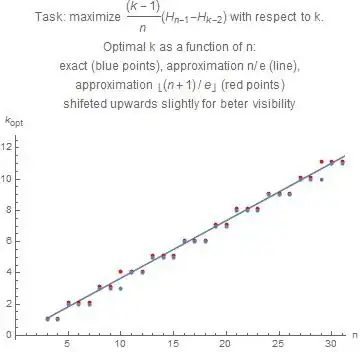
During an excercise session in a basic course of probability it was shown that the secretary problem can be reduced to solving the following task: For a given natural $n$ optimize $2\leq k\leq n-1$ so that $\frac{k-1}{n}\sum^n_{i=k}\frac 1{i-1} = \frac{k-1}{n}(\operatorname{H}_{n-1}-\operatorname{H}_{k-2})$ is the largest.

Solution that was presented to me:

$\operatorname{H}_l=\operatorname{ln}l+\lambda+\operatorname{o}(1)$

$\frac{k-1}{n}(\operatorname{H}_{n-1}-\operatorname{H_{k-2}})\approx\frac{k-1}n (\operatorname{ln}(n-1)-\operatorname{ln}(k-2))$

$f(k):=(k-1)\operatorname{ln} n-(k-1)\operatorname{ln}(k-1)$

$f^{\prime}(k)=\operatorname{ln}n-\operatorname{ln}(k-1)-1$

$f^{\prime}(k)=0\iff k=\frac{n}{\operatorname{e}}+1$

So the optimal $k$ is $\frac n {\operatorname{e}}+1$ and for this $k$ we have $\frac{k-1}n (\operatorname{ln}(n-1)-\operatorname{ln}(k-2))=\frac n {\operatorname{e}}$

It is likely because I've already forgotten quite a lot from my elementary courses on fields like mathematical analysis and discrete mathematics that I don't think I understand the above proof.

For me this proof leaves significant holes. First and foremost, the fact that

$\operatorname{H}_l=\operatorname{ln}l+\lambda+\operatorname{o}(1)$

does not yet prove that

$\frac{(k+1)-1}{n}(\operatorname{H}_{n-1}-\operatorname{H_{(k+1)-2}})>\frac{k-1}{n}(\operatorname{H}_{n-1}-\operatorname{H_{k-2}})\iff \\\frac{(k+1)-1}n (\operatorname{ln}(n-1)-\operatorname{ln}((k+1)-2))>\frac{k-1}n (\operatorname{ln}(n-1)-\operatorname{ln}(k-2))$

And this is a prerequisite of studying the monotonicity of $\frac{k-1}{n}(\operatorname{H}_{n-1}-\operatorname{H_{k-2}})$ by means of studying the monotonicity of $\frac{k-1}n (\operatorname{ln}(n-1)-\operatorname{ln}(k-2))$.

This $\operatorname{o}(1)$ tells us that any inaccuracies become insignificant for sufficiently large $k$; but we don't have "sufficiently large $k$" - on the contrary, we have $2\leq k\leq n-1$. So instead of saying anything about "sufficiently large $k$" we should prove that the inaccuracies are insignificant enough not to affect the result of our computations for $k$ as low as $3$!! and I don't know how to prove this.

We have:

$\frac{(k+1)-1}{n}(\operatorname{H}_{n-1}-\operatorname{H_{(k+1)-2}})>\frac{k-1}{n}(\operatorname{H}_{n-1}-\operatorname{H_{k-2}})\iff\operatorname{H}_{n-1}-\operatorname{H}_{k-2}>k(\operatorname{H}_{k-1}-\operatorname{H}_{k-2})\iff\\\operatorname{ln}(n-1)-\operatorname{ln}(k-2)+\operatorname{o}(1)>k(\operatorname{ln}(k-1)-\operatorname{ln}(k-2)+\operatorname{o}(1))$

And why can we simply discard these $\operatorname{o}(1)$s in the above expression?

What am I missing? What did I forget?

Answer 1

EDIT: graph and approximation improved

The following graph compares the exact optimal value of k with the approximations $k_{appr1} = n/e$ and $k_{appr2}=\left\lfloor (n+1)/e\right\rfloor$

We gather from the graph that $k_{appr2}$ is an almost pointwise correct approximation to $k_{opt}$ which fails only in very few points at the ends of the steps of the "staircase" (see $n=10$ and $n=29$).

Answer 2

A heuristic "justification" is that applying the approximation leads us to the guess $k \approx n/e + 1$, which is large when $n$ is large. So the large $k$ approximation is at least consistent with the result obtained.

Certainly more work needs to be done to justify that the maximum is not actually elsewhere -- the "solution" you were presented is not a rigorous one, but I don't think it was intended to be viewed as rigorous in the first place. Further, the approximation $H_n \approx \log n + \gamma$ is off by at most $0.23$, which is small enough to believe that the result obtained is close to correct.