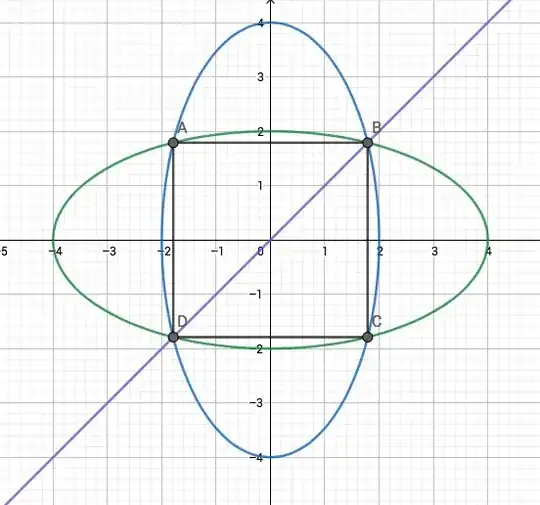
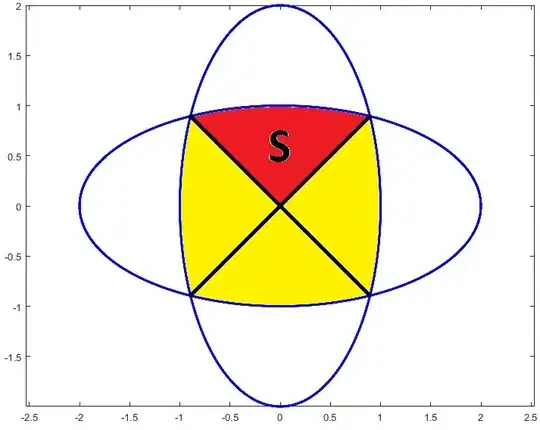
I'm trying to find the area inside the intersection of the region bounded by the ellipses $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ and $\frac{x^2}{b^2}+\frac{y^2}{a^2}=1$ using vector calculus methods.
I understand how to calculate area of regions by taking the line integral around the boundary and using Green's Theorem. However what I'm stuck with is finding a paramterization of the boundary! Can anyone point me in the right direction?