identity for finding value of $\pi$

Question

So in Euler's solution of the Basel problem he takes $\sin x= x\left(1-\frac{x^2}{\pi^2}\right)\left(1-\frac{x^2}{4\pi^2}\right)\cdots$

well, i was playing around with it and put $ x=\frac{\pi}{2}$

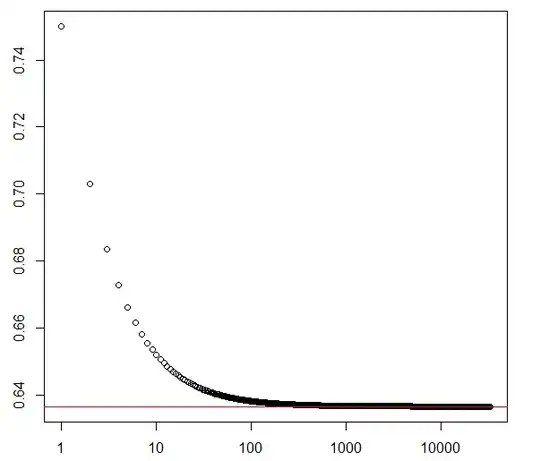
After manipulating quite a bit, $$\frac{2}{\pi}=\left(1-\frac{1}{2^2}\right)\left(1-\frac{1}{(2*2)^2}\right)\cdots\left(1-\frac{1}{(2n)^2}\right)\cdots$$ after simplifying a bit$$\frac{2}{\pi}=\left(\frac{3}{4}\right)\left(\frac{15}{16}\right)\left(\frac{35}{36}\right)\left(\frac{99}{100}\right)\cdots$$

I tried evaluating LHS by hand, and the partial products slowly do decrease towards RHS, and we know that they will not decrease forever because $$\lim_{n\to\infty} \frac{n^2-1}{n^2}=1$$ so can anyone help by writing a program which can do partial sum up to high values of n and tell me if its true. PS.I am in 10th standard do if im wrong anywhere please dont explain in too complicated mathematics. thanks

It's a known result, Wallis product, though Wallis didn't prove it that way (predictably, since he did so in 1655, long before Euler's results). — , Jan 15 '18 at 18:30
well, i couldn't find anything by "2/pi infinite product identity" on google so i posted it here. thank you for directing me. — user167920, Jan 15 '18 at 18:34
i know how to prove the euler product identity i wanted to know if the identity i reached was true or if i made some mistake — user167920, Jan 15 '18 at 18:54

score 1 · Accepted Answer · answered Jan 15 '18 at 18:32

1

$\dfrac2{\pi} \approx 0.6366198$ is the correct limit of the product

As an illustration (not a proof) using R:

maxn  <- 2^15
plot(exp(cumsum(log(1 - (2*(1:maxn))^(-2)))), log="x")
abline(h=2/pi, col="red")

giving

answered Jan 15 '18 at 18:32

Henry

157,058

thank you, for the program mister henry – user167920 Jan 15 '18 at 18:54

identity for finding value of $\pi$

1 Answers1