2

Is the following Proof Correct?

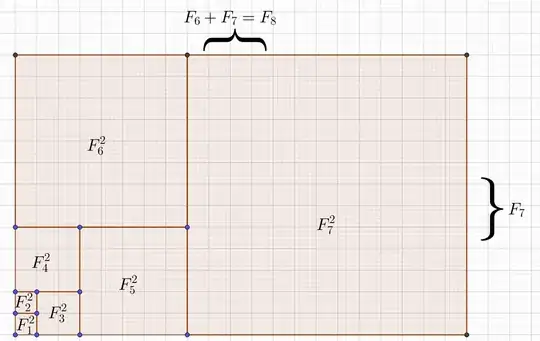
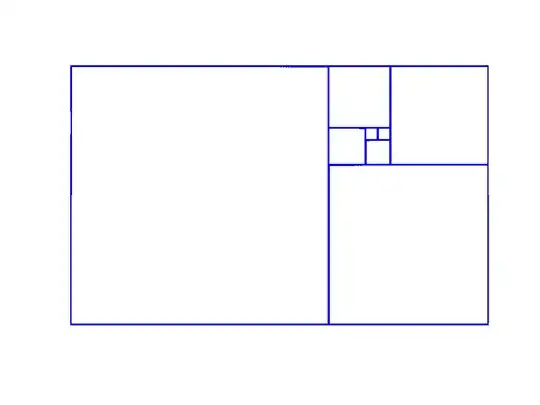
Theorem. Consider the following statement. $$\forall n\in\mathbf{N}\left(\sum_{j=0}^{n}(F_i)^2 = F_nF_{n+1}\right)$$ Proof. We prove the statement by recourse to Strong-Induction. Assume for an arbitrary natural number $n$ that $$\forall n<k\left(\sum_{j=0}^{k}(F_i)^2 = F_kF_{k+1}\right)$$ Now consider the following Cases.

Case-1: $n = 0$,then since $F_0 = 0$ we have $\sum_{i=0}^{0}(F_i)^2 = (F_0)^2 = 0^2 = 0 = 0\cdot F_1 = F_0F_1$.

Case-2: $n = 1$, then since $F_1 = 1$ we have $\sum_{i=0}^{0}(F_i)^2 = (F_0)^2+ (F_1)^2 = 0^2 +1^2 = 1 = 1\cdot(1+0) = F_1\cdot F_2$

Case-3: $n \ge 2$,then by considering the inductive hypothesis in the particular for $k = n-1$ we see that $$\sum_{j=0}^{n}(F_i)^2 = \sum_{j=0}^{k}(F_i)^2 +(F_n)^2 = F_{n-1}F_n+(F_n)^2$$ from this point onwards we must show that $F_{n-1}F_n+(F_n)^2 = F_nF_{n+1}$, instead we prove the equivalent statement $(F_n)^2 = F_nF_{n+1}-F_nF_{n-1}$, equivalently we have $F_{n}\cdot(F_{n+1}-F_{n-1})$ from definition of the Fibonacci sequence we know that $\forall n\ge 2(F_{n+1} = F_{n}+F_{n-1})$ consequently we have $F_{n} = F_{n+1}-F_{n-1}$ implying that $F_n\cdot(F_{n+1}-F_{n-1}) = F_n\cdot F_n = (F_n)^2$.

atifcppprogrammer
  • 5,852

3 Answers3

11

From the figure below the theorem's proof comes. The rectangle's area is $F_{i}F_{i+1}$.

enter image description here

Pet123
  • 1,252
  • 2
    This doesn't address the question asked, which was if the OP's proof was correct. While I think it is often appropriate to supply additional information such as this, you should always state that you are doing so instead of answering the question. – Paul Sinclair Jan 21 '18 at 04:50
9

Your proof looks correct apart from some typos: $\forall n<k$ should be $\forall k < n$, and (as @mathlove noticed) there is a mix-up between $i$ and $j$ in the indices.

But it can be simplified. In particular you don't need strong induction since only the inductive hypothesis for $n-1$ is used to prove the statement for $n$, so “simple induction” is sufficient.

Also $F_{n+1} = F_{n}+F_{n-1}$ holds for $n\ge 1$ and not only for $n \ge 2$, therefore it is sufficient to consider a single base case ($n = 0$).

For $n \ge 1$ the inductive step then would be: From the inductive hypothesis we have $$ \sum_{i=0}^{n-1}(F_i)^2 = F_{n-1}F_n \, . $$ It follows that $$ \sum_{i=0}^{n}(F_i)^2 = F_{n-1}F_n+(F_n)^2 = (\underbrace{F_{n-1} + F_n}_{F_{n+1}}) F_n = F_{n+1}F_n \, . $$ In the final step, the recurrence relation of the Fibonacci numbers is used directly, without transformation to an “equivalent statement”.

Martin R
  • 113,040
0

This identity can be seen readily in the Fibonacci mosaic below. Clearly, the area of the overall rectangle, $F_{n+1}\times F_{n}$ is the sum of the areas of the individual squares $F_{k}\times F_{k}$ from $k=1:n$.

Fibonacci Mosiac

Cye Waldman
  • 7,524
  • 2
    This does not address the question asked and was posted over an hour after Pet123's post, from which it differs only in arranging the squares in a spiralling pattern instead of building from a corner. What was the point? – Paul Sinclair Jan 21 '18 at 04:53
  • @PaulSinclair Thanks for your comment. (1) I didn't see Pet123s at the time I typed this up and (2) my diagram is actually the template for the Fibonacci spiral and is more recognizable and well known. As for why I didn't see the post, I had the page open for over an hour while I falsely pursued the identity $\sum_1^n F_kF_{k-1}=F_n^2,~n \text{ even}$ with another mosaic. – Cye Waldman Jan 21 '18 at 16:33