3

Problem from Calculus with Analytic Geometry 2nd ed. from Simmons, page 87/21(c).

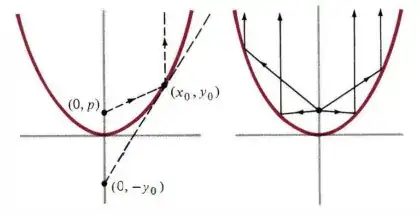
Let $p$ be a positive constant and consider the parabola $x^2 = 4py$ with vertex at the origin and focus at the point $(0, p)$. Let $(x_0, y_0)$ be a point on this parabola other than the vertex. Assume we've proved

  • tangent at $(x_0, y_0)$ has $y$-intercept $(0, -y_0)$
  • triangle with vertices $(x_0, y_0), (0, -y_0), (0, p)$ is isosceles.

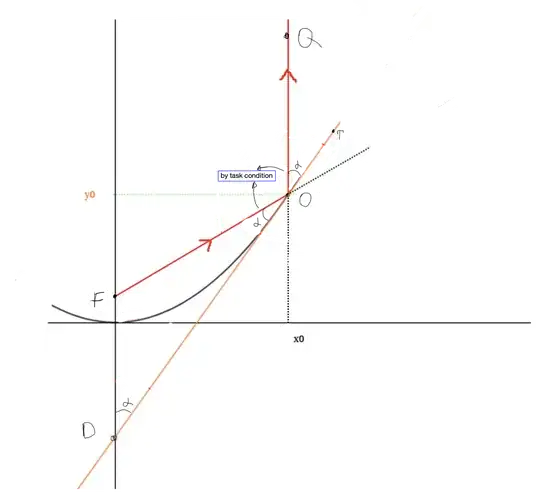
Now suppose that a source of light is placed at the focus of a parabola, and assume that each ray of light leaving the focus is reflected off the parabola in such a way that it makes equal angles with the tangent line at the point of reflection (the angle of incidence equals the angle of reflection). Use (b) to show that after reflection each ray points vertically upward, parallel to the axis.

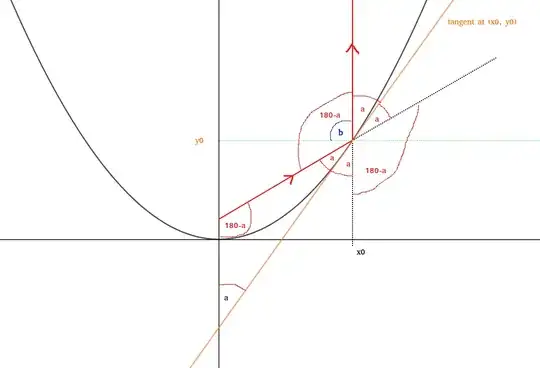
enter image description here

My analysis is here. But I don't know how to prove that angle $b = 90 \deg$: enter image description here

José Carlos Santos
  • 427,504
pseudomarvin
  • 861
  • 1
    You mean $180-2a$? –  Jan 22 '18 at 15:52
  • 1
    You're not going to have much luck in showing $b$ is 90 degrees. How would you recover $b$ using only $a$ (especially since $a$ may vary)? It's a theorem in classical geometry that if you have two lines that are cut by a transversal line, then the two original lines are parallel if and only if the transversal cuts equal corresponding angles at the points of intersection. You've already shown this. More information on this wiki page: https://en.wikipedia.org/wiki/Transversal_(geometry) –  Jan 22 '18 at 19:21
  • 1
    Does this answer your question? Geometric/analytic proof of the parabola mirror focus – tryst with freedom Aug 05 '21 at 05:15

2 Answers2

1

Here is a purely analytical solution. Canonical parabola equation is

$$ y^2=2px $$

with focus in $(p/2,0)$. The tangent line to point $(x_0,y_0)$ is

$$ px - y_0 y+px_0=0 $$

That is all we need. Tangent line directional vector is $\vec{u}=\{y_0,p\}$. Vector $\vec{v}=\{p,-y_0\}$ is orthogonal to $\vec{u}$ and $u=|\vec{u}|=|\vec{v}|$. Consider vector $\vec{q}=\{p/2-x_0,0\}$ directional for the line coming through the focus $(p/2,0)$ and point $(x_0,y_0)$ belonging to the parabola. Its decomposition in directions of $\vec{u}$ and $\vec{v}$ looks as follows:

$$ \vec{q}=\frac{\vec{q}\cdot\vec{u}}{uq}\vec{u}+\frac{\vec{q}\cdot\vec{v}}{uq}\vec{v} $$

Now the important part: directional vector $\vec{q}'$ of the reflection would have $\vec{u}$-component opposite to that of $\vec{q}$ and $\vec{v}$-component the same. Thus,

$$ \vec{q}'=-\frac{\vec{q}\cdot\vec{u}}{uq}\vec{u}+\frac{\vec{q}\cdot\vec{v}}{uq}\vec{v} $$

All it's left is to calculate the relevant dot-products and to see that $y$-component of $\vec{q}'$ is zero. The dot-products:

$$ \vec{q}\cdot\vec{u}=(p/2-x_0)y_0-y_0p=-y_0(x_0+p/2) $$

and

$$ \vec{q}\cdot\vec{v}=(p/2-x_0)p+y_0^2=p/2-px_0+2px_0=p(x_0+p/2) $$

Finally, $y$-component of $\vec{q}'$ is

$$ \frac{1}{qu}\left[y_0(x_0+p/2)p+p(x_0+p/2)(-y_0)\right]=0 $$

QED

mobiuseng
  • 251
1

You have that triangle with vertices $(_0,_0),(0,−_0),(0,)$ is isosceles. Also you have that the angle of incidence is equal to the angle of reflection.

It is easy to prove that two lines are parallel if the corresponding angles formed by Transversal line are equal.

So y-axis and line $OQ$ with transversal line $OT$ which is tangent line in this case have equal corresponding angles $\angle ODF$ = $\angle TOQ$

enter image description here

Harish Chandra Rajpoot
  • 37,450
Zhirayr Ayrapetyan
  • 45
  • 5