5

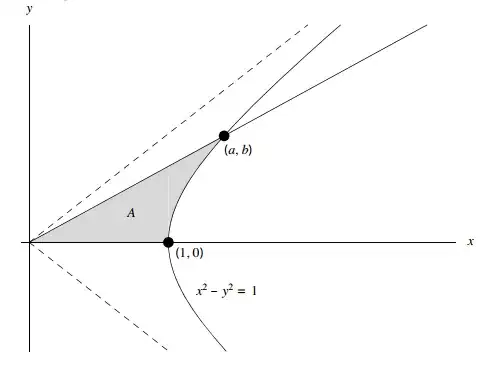
I'm trying to derive the definitions of hyperbolic functions with this image in mind, where $a := \cosh u$, $b := \sinh u$, and $u = 2A$.

I have $$2A = 2\int_{0}^b \sqrt{1+y^2} \ \mathrm{d}y = b\sqrt{b^2 + 1} + \log\left(b + \sqrt{b^2 + 1}\right)$$ and therefore $$\begin{align} \cosh u &= \cosh\left(\;b\sqrt{b^2 + 1} + \log\left(b + \sqrt{b^2 + 1}\right)\;\right) = \sqrt{b^2 + 1} \\ \sinh u &= \sinh\left(\;b\sqrt{b^2 + 1} + \log\left(b + \sqrt{b^2 + 1}\right)\;\right) = b \end{align}$$

The goal here is to solve for $u$ in terms of $b$ and then derive the usual formulas, but that's proven to be impossible (unless I made a mistake, which I think might be the case here). Where can I go from here?

Also, I'm using the derivation shown in this guide.

EDIT: The correct integral is $$2A = 2\int_{0}^b \left( \sqrt{1+y^2} - \frac{a}{b}y \ \mathrm{d}y \right) = \log\left(b + \sqrt{b^2 + 1}\right)$$ so $$b = \cfrac{e^{2u} - 1}{2e^u}$$ and from here the rest follows trivially.

Matheus Andrade
  • 6,773

1 Answers1

5

Don't forget that the region $A$ is sliced off by the line $x=\frac ab y$, so you should amend your integral to be $$ 2A = 2\int_{0}^b \left(\sqrt{1+y^2}-\frac ab y\right) dy.\tag1$$ But since $(a,b)$ lies on the hyperbola, we have $a=\sqrt{b^2+1}$. Plugging this in to (1) and evaluating the integral, you'll end up with $$u=2A=\log(b+\sqrt{b^2+1}).\tag2$$ (Note that this amendment amounts to subtracting off double the area of a right triangle with legs $a$ and $b$.)

Your next step is to solve (2) for $b$ in terms of $u$.

grand_chat
  • 38,951