Edit. First version lacked clarity and had some errors.
First note that
\begin{align}
I_n(t) =\frac{1} {i2} \int^\infty_0 x^{n-1}e^{(i-t) x} \,dx - \frac{1} {i2} \int^\infty_0 x^{n-1}e^{(-i-t) x} \,dx
\end{align}
We have two integrals. Both can be related to a contour integral. One also can see somehow the $\Gamma$-function in it, so it would be very nice to expres these integrals in terms of $\Gamma$-function. That is what we will do and we only show it for the first integral. For that consider:
\begin{align}
\tag{1}
\oint_C z^{n-1}e^z\, dz
\end{align}
The contour $C$ is a circle sector with angle $\arctan(1/t)$ going from the origin all the way up in the second quadrant and coming back all the way down through the negative real axis. Let the radius of the "circle" be $R$. The contour can be seen below.
$\hspace{70pt} $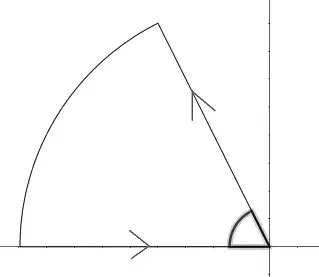
When $R$ goes to infinity the circular contribution goes to zero by the ML-lemma. Since the integrand is holomorphic, by Cauchy's theorem we get that the integral in $(1)$ is zero and by parameterization (and taking $R\to \infty $) :
\begin{align}
\int^0_{-\infty}x^{n-1}e^x\, dx+(i-t)^n\int^\infty_0 x^{n-1}e^{(i-t) x} \, dx=0
\end{align}
We substitute $u=-x$ for the first integral:
\begin{align}
\int^\infty_{0}(-1)^{n-1}u^{n-1} e^{-u}\,du + (i-t)^n\int^\infty_0 x^{n-1}e^{(i-t) x} \, dx=0
\end{align}
Ladies and gentleman, that is what we just wanted: the first integral is the $\Gamma$-function and all that implies:
\begin{align}
\frac{1} {i2} \int^\infty_0 x^{n-1}e^{(i-t) x} \,dx=\frac{(n-1)!(-1)^{n}} {i2(i-t)^n} =\frac{(n-1)!(t+i)^n}{i2(1+t^2)^n}
\end{align}
Similary we get:
\begin{align}
\frac{1} {i2} \int^\infty_0 x^{n-1}e^{(-i-t) x} \,dx=\frac{(n-1)!(t-i)^n}{i2(1+t^2)^n}
\end{align}
Adding them up yields the desired result.
