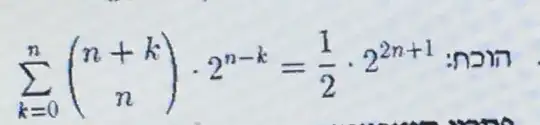Algebraically prove that $\sum\limits_{k=0}^n {n+k \choose n}\mathrm{2}^{n-k} = 1/2 \cdot \mathrm{2}^{2n+1}$

Question

write the most simple algebraic proof you can, that means no integrals and no exponential generating functions if possible. I have tried to solve it for close to 2 hours. what I got to is almost nothing but here it is : $1/2 * \mathrm{2}^{2n+1}=\mathrm{2}^{2n}=\mathrm{4}^n=\mathrm{(2+2)}^n= \sum_{k=0}^n\binom{n}{k}\mathrm{2}^k\mathrm{2}^{n-k}=?\sum_{k=0}^n {n+k \choose n}\mathrm{2}^{n-k} $ and that's it. this is the first time I tried to use symbols so if something goes wrong, I am terribly sorry.

Why write $\frac 12 \times 2^{2n+1}$? That seems an odd way to write $2^{2n}$, no? — lulu, Feb 10 '18 at 01:05
Also, the problem in the text doesn't match the problem in the header so... — lulu, Feb 10 '18 at 01:10
Have you tried to prove this by induction on $n?$ I haven't tried it myself, but it seems like a possible line of attack. — saulspatz, Feb 10 '18 at 01:11
they want me to prove it combinatorially after the algebraic proof. I assumed it was easier to do that proof with it written this way. — Mohammad Amer, Feb 10 '18 at 01:11
@lulu fixed the header. haven't tried induction, will do now. — Mohammad Amer, Feb 10 '18 at 01:13
If they want you to prove it combinatorially, have you considered what either side of the equation could be counting? — Steven Stadnicki, Feb 10 '18 at 01:33
@StevenStadnicki I have. but I really want to solve it algebraically first. I thought it might be counting how many binary strings there are over length 2n. — Mohammad Amer, Feb 10 '18 at 01:35

Rohan Shinde · Accepted Answer · 2018-02-10T03:34:25.733

Hint:

You could try it as follows

The given expression can be written as $$2^n \sum_{k=0}^n \binom {n+k}{n}\cdot 2^{-k}$$

This can also be written as $$2^n \cdot \text {coefficient of $x^n$ in the expansion } \left[\left( \frac {1}{2}+x\right)^n +\left( \frac {1}{2}+x\right)^{n+1}+ \cdots +\left( \frac {1}{2}+x\right)^{2n}\right]$$

We can also add the remaining terms of the series inside the bracket because nevertheless they are not going to give the coefficient of $x^n$ in their expansion.

Hence we need to find $$2^n \cdot \text {coefficient of $x^n$ in the expansion } \left[\left( \frac {1}{2}+x\right)^0 +\left( \frac {1}{2}+x\right)^{1}+ \cdots +\left( \frac {1}{2}+x\right)^{2n}\right]$$

Now whatever inside the square bracket is nothing but a Geometric progression written out there which can be easily summed.

I hope you can take it from here.

Algebraically prove that $\sum\limits_{k=0}^n {n+k \choose n}\mathrm{2}^{n-k} = 1/2 \cdot \mathrm{2}^{2n+1}$

1 Answers1