0

I am considering the polynomial $$ p(c,x):=x^{c+1}-x^c-1 $$ By $x_c$ denote the largest positive real root of $p(c,x)$.

From mathematics we know that $x_c\in (1,1+\frac{\log(c)}{c})$ and that, for large $c$, $x_c$ behaves like $1+\frac{\log(c)}{c}$ which means, in mathematical terms, that $x_c\sim 1+\frac{\log(c)}{c}$ as $c\to\infty$ or more formally: $$ \lim_{c\to\infty}\frac{x_c}{1+\frac{\log(c)}{c}}=1. $$

My numerics show that we also seem to have $$ \lim_{c\to\infty}\frac{x_c}{1+\frac{1}{c}}=1. $$

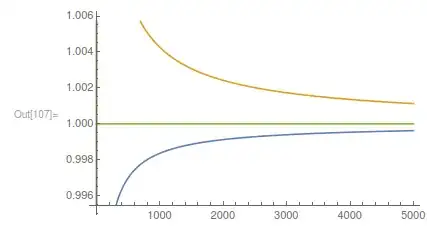
In the following picture, the blue curve is the function $$ f(c)=\frac{x_c}{1+\frac{\log(c)}{c}} $$ and the orange curve is the function $$ g(c)=\frac{x_c}{1+\frac{1}{c}}. $$

It seems that the blue curve reaches the value 1 faster than the orange curve.

Does this mean that it is better to say that $$ x_c\sim 1+\frac{\log(c)}{c}, c\to\infty $$ than to say that $$ x_c\sim 1+\frac{1}{c}, c\to\infty? $$

Note $\frac{1}{c}\leq\frac{\log(c)}{c}$ for large $c$. So I would have expected that $1+\frac{1}{c}$ is a better approximation.

Asymptotics as c goe to infinity

Antonio Vargas
  • 24,993
mathfemi
  • 2,631
  • I outlined a proof in this answer for the asymptotic $$x_c = 1 + \frac{W(c+1)}{c+1} + \frac{W(c+1)^2}{2(c+1)^2} + o!\left(\frac{(\log c)^2}{c^2}\right)$$ as $c \to \infty$, where $W$ is the Lambert W function. From this we can deduce, for example, that $$x_c = 1 + \frac{\log c-\log\log c}{c} + o!\left(\frac{1}{c}\right)$$ as $c \to \infty$. – Antonio Vargas Feb 25 '18 at 21:47

2 Answers2

1

Note $\frac{1}{c}\leq\frac{\log(c)}{c}$ for large $c$. So I would have expected that $1+\frac{1}{c}$ is a better approximation.

For all you know, $x_c$ could be equal to $1+\frac{1}{c}$, and it could as well be equal to $1+\frac{\log c}{c}$. All of what you said would still hold. Except that obviously the "best" approximation in not the same in both cases. So you should not expect $\frac{1}{c}\leq\frac{\log(c)}{c}$ to tell you anything about which approximation is the best.

Secondly, note that $$\lim_\limits{c\to \infty}\frac{1+\frac{\log(c)}{c}}{1+\frac{1}{c}}=1$$ therefore any sequence equivalent to the numerator is also equivalent to the denominator. Which of these approximations is the "best" depends on the sequence. You can't tell anything more without looking at higher order terms.

Arnaud Mortier
  • 27,276
  • Isn't $\frac{1}{c}\in o(\frac{\log(c)}{c})$ as $c\to\infty$? – mathfemi Feb 25 '18 at 13:43
  • Yes it is. But this in now way interferes with what I wrote. Equivalence has its limitations. – Arnaud Mortier Feb 25 '18 at 13:45
  • @mathfemi if you will, $0\in o(\frac{1}{c})$ as well, therefore $1$ is yet a better approximation, according to that logic. – Arnaud Mortier Feb 25 '18 at 13:47
  • I am just confused because the numerics seem to indicate that $1+\frac{\log{c}}{c}$ is better approximating the sequence $x_c$, Since $x_c\to 1$ this seems to mean that $\log(c)/c$ tends to $0$ more quickly than $1/c$ but thats obviously not true. – mathfemi Feb 25 '18 at 13:51
  • @mathfemi Again, imagine that $x_c$ was equal to $1+\frac{\log c}{c}$. What better approximation than that could you imagine? Yet $\log (c) /c$ still converges to $0$ less quickly than $1/c$. So you see that the two things are totally unrelated. – Arnaud Mortier Feb 25 '18 at 13:57
  • Okay, so for my situation I can only state that $x_c\sim 1+\frac{1}{c}$ and $x_c\sim 1+\frac{\log c}{c}$ as $c\to\infty$ and that numercis suggest that the first approximation is better. – mathfemi Feb 25 '18 at 14:04
  • @mathfemi Yes, precisely. – Arnaud Mortier Feb 25 '18 at 14:18
1

No

When you say

$$\lim_{c\to\infty}\frac{x_c}{1+\frac{\log(c)}{c}}=1 \text{ and } \lim_{c\to\infty}\frac{x_c}{1+\frac{\log(c)}{c}}=1$$

this is hard a surprise since $x_c \to 1$ as $c$ increases.

The fact that your blue line is closer to the green line than the orange line is suggests that $1+\frac{\log(c)}{c}$ is a better approximation to $x_c$

Henry
  • 157,058