Simulating a divide area random variable

Question

Suppose that we have a random variable with pdf like $f = \left\{ \begin{array}{ c l } x+1, x\in [-1,0] \\ -x+1, x\in (0,1] \end{array} \right.$ and we have to simulate it.

It's pdf is $F(x) = \left\{ \begin{array}{ c l } x^2/2+x+0.5, x\in [-1,0] \\ -x^2/2+x+0.5, x\in (0,1] \end{array} \right.$

two methods to simulate this can be found here http://web.ics.purdue.edu/~hwan/IE680/Lectures/Chap08Slides.pdf page 12.

My question is if we can simulate problems like that by fist simulate a random U(0,1) and

if it is smaller than the probability $P(x\in [-1,0])=1/2$ simulate from the first part with inverse transformation $\sqrt{2U}-1$ but for a $U\sim Unif(0,1/2=P(x\in [-1,0]))$

and if it is bigger simulate with inverse transformation $1-\sqrt{(2(1-U))}$ using a $U\sim Unif(1/2,1)$.

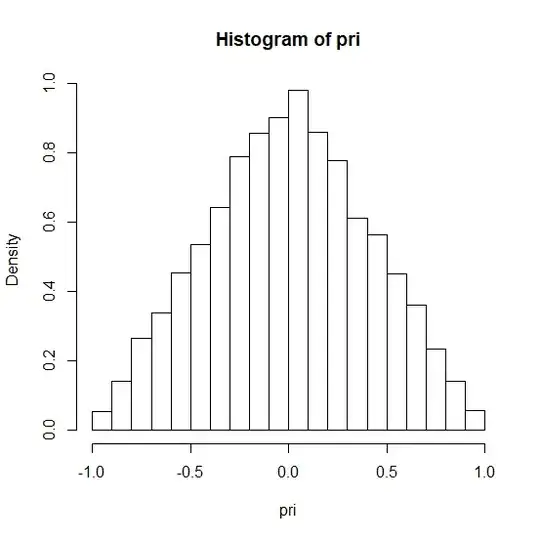
When I make the histogram it seems to working, but is it correct?

[code]rand=function(){
if(runif(1,0,1)<=1/2){x=sqrt(2*runif(1,0,1/2))-1}else{
x=1-sqrt(2-2*runif(1,1/2,1))
}
return(x)
}


pri=NULL


for(i in 1:10000)
{
pri=c(pri,rand())
}


hist(pri,prob=T)[/code]

Though Kolmogorov used small letters to denote random variables in his book, I suggest using capital letters for theoretical stuff like events $E$ and random variables $X,U$, and small letters for observations like an instance $x$ of $X$ and the sample mean $\bar{x}_n$. — GNUSupporter 8964民主女神地下教會, Mar 01 '18 at 12:07

score 1 · Accepted Answer · answered Mar 01 '18 at 13:23

Yes, your code generates the correct results, but as you can see from the calculations below, it's hard to understand. I suggest sticking with the linked lecture notes and use runif(1,0,1), which represents $\mathrm{Unif}(0,1)$.

The composition algorithm in the linked notes:

Generate two independent $U_1, U_2 \sim \mathrm{Unif}(0,1)$

If $U_1 < 1/2$, return $X = \sqrt{U_2}-1$

Otherwise, return $X = 1 - \sqrt{1-U_2}$

The composition algorithm in the question body contains a rescaled version of $U_2$.

Generate $U_1 \sim \mathrm{Unif}(0,1)$

$U_1 < 1/2$, return $X = \sqrt{2U}-1$ for $U\sim \mathrm{Unif}(0,1/2)$
In fact, $2U \stackrel{(d)}{=} U_2$.

Otherwise, return $X = 1 - \sqrt{2-2U}$ for $U\sim \mathrm{Unif}(1/2,1)$
In fact, $2U \sim \mathrm{Unif}(1,2)$, so $2-2U \sim \mathrm{Unif}(0,1)$ and $2-2U \stackrel{(d)}{=} 1-U_2$.

These figures illustrates the how the code works.

If we increase the sample size from 10k to 50k, the histogram looks more similar to the triangular distribution on $[-1,1]$.

We increasing the class number from 20 to 50 in order to take a closer look of the data.

My code

rand=function(){
if(runif(1,0,1)<=1/2){x=sqrt(2*runif(1,0,1/2))-1}else{
x=1-sqrt(2-2*runif(1,1/2,1))
}
return(x)
}

pri=NULL
for(i in 1:50000)
{
pri=c(pri,rand())
}

hist(pri,breaks=50,prob=T)

Thank you for your answer. I tried to find a way to prove that we can work like this (like the one I posted) in all the similar problems, but I couldn't prove something that will work on every case. Anyway thanks again. — papasmurfete, Mar 04 '18 at 16:43

Simulating a divide area random variable

1 Answers1