Struggling with this permutations question:
In how many ways can one yellow, two red and four green beads be placed on a bracelet if the beads are identical apart from colour?
Apparently you need to consider cases but I'm not quite sure how to go about doing that. Also, is there a way to do it without cases (i.e. a general formula)?
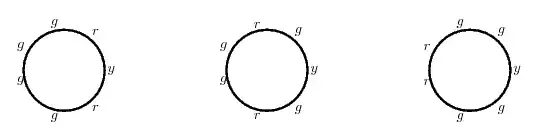
Since there is a single yellow bead, we can use it as a reference point. As we proceed clockwise around the bracelet from the yellow bead, we must choose which two of the remaining six positions will be filled with red beads. There are $$\binom{6}{2} = 15$$ ways to do this.
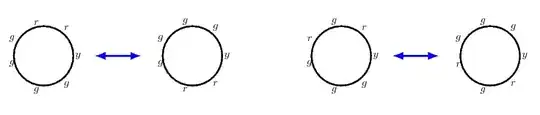
However, a bracelet can be removed from the wrist, twisted, and placed back on the wrist. Consequently, clockwise and counterclockwise (anticlockwise) arrangements are equivalent. Of these $15$ arrangements, the three in which both red beads are equidistant from the yellow bead are the same when the bracelet is reversed. The other $12$ are not. They can be placed in $6$ matching pairs, so there are $3 + 6 = 9$ distinguishable bracelets that can be formed.
The finished nonoriented bracelet is an adorned cyclic graph with $7$ vertices, up to isomorphy. The two red beads have distance $1$, $2$, or $3$ in this graph. For any choice of this distance, up to isomorphy there are three places left for the yellow bead, one of them in symmetric position with respect to the red beads. It follows that one can make $3\cdot3=9$ such bracelets out of the given beads.
