5

For university I have to construct equivalent Mealy and Moore machines that solve certain problems. But I am confused, as my Moore and Mealy machines turn out to have exactly the same nodes, just with different labels.

Example

  • Input alphabet: {0, 1, ..., 9}
  • Output alphabet: {0, 1}
  • Function: Output 1 if the current number is divisible by 3, else output 0.

Moore

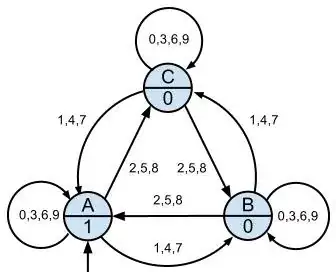
enter image description here

Mealy

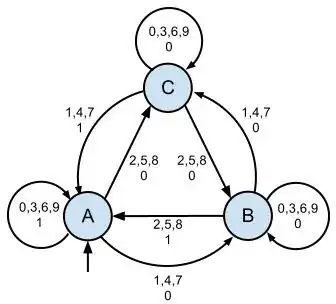
enter image description here

You see, all I did for creating the Mealy machine was moving the output from the nodes to the connections. Which would make it quite trivial to convert an arbitary Moore machine to a Mealy machine.

Possible sources of my confusion:

  1. My understanding of the differences between the two types is fundamentally flawed.
  2. The conversion Moore => Mealy is in fact trivial.
  3. This example is a special case where the Mealy and Moore machines look the same.
  4. There is a simpler Mealy machine than the one I built here.
  5. My Moore machine is not a valid Moore machine. / My Mealy machine is not a valid Mealy machine. (see 4)

I tried to start from scratch building the Mealy machine, but as I found Moore much easier to build I am always biased towards the Moore solution.

Lucius
  • 153
  • 1
    A Moore machine is (essentially, you need to add labels) a Mealy machine. The Moore outputs are a function of state (only), whereas the Mealy outputs may change with inputs. A Mealy machine can always be converted to a Moore machine, with the possible addition of extra states. – copper.hat Jan 02 '13 at 00:09
  • 1
    This renders the excercise of building a Moore and a Mealy machine for the same problem kind of pointless. Unless my professor only wants to test my ability to draw diagrams. – Lucius Jan 02 '13 at 00:10
  • 1
    Or maybe your professor intended for you to have this realisation! – Alex J Best Jan 02 '13 at 00:26
  • Well, not entirely, I haven't tried to figure out what your machine accepts, but it is possible that a Mealy machine may have fewer states. – copper.hat Jan 02 '13 at 00:26
  • 1
    A brief glance at your machine suggests to me that you need a minimum of 3 states, so the above seems reasonable. It seems to be counting the number of times ${2,4,7}$ is seen less the number of times ${1,4,7 }$ is seen, and outputs $1$ iff the count is $0$ modulo $3$. Hence $3$ states are needed at minimum. – copper.hat Jan 02 '13 at 00:32
  • 1
    @Alex: There are two excerises that require me to build a Mealy and a Moore machine for the same problem. I wonder if my professor thought that it is necessary to have this realisation twice. Otherwise I still don't see the point. – Lucius Jan 02 '13 at 00:44
  • @copper.hat: For building the machines I used the fact that divisible by 3 is equivalent to the cross total is divisible by 3. An input of 627 outputs 101, as 6 % 3 = 0, 62 % 3 = 2 and 627 % 3 = 0 (% is the modulo operator). The modulos are simply added for each new digit in the input stream. – Lucius Jan 02 '13 at 00:44
  • Cute! In any case, you need at least 3 states, so the best a Mealy machine will get you is a faster output. – copper.hat Jan 02 '13 at 00:50
  • It's not the end of the world if I get this excercise wrong. At least I am now confident enough with my understanding of the problem that I can hand this in. Thank you very much! – Lucius Jan 02 '13 at 00:56

1 Answers1

3

The only difference between a Moore machine and a Mealy machine is how the output of the machine is defined. In a Moore machine, the output is based solely off the current state. In the formal definition, we say that there is an output function $$ G:S\rightarrow \Lambda $$ where $S$ is the set of states and $\Lambda$ is the output alphabet (i.e. the set of symbols that could possibly be output). So this function $G$ takes a state and outputs a symbol. In a Mealy machine, the output is based off of the current state and the current input. In the formal definition, we say that there is an output function $$ G:S\times\Sigma\rightarrow \Lambda $$ where $S$ is the set of states, $\Sigma$ is the input alphabet (i.e. the set of symbols that could possibly be input), and $\Lambda$ is the output alphabet. So this function $G$ takes a pair, one state and one input symbol, and outputs a symbol.

We can see by this definition that a Moore machine is just a special type of Mealy machine such that the Mealy machine's input symbol is ignored in the output. If we wanted to turn a Moore machine into a Mealy machine, we would change our function $G_1:S\rightarrow \Lambda$ to a function $G_2:S\times\Sigma\rightarrow \Lambda$ so that for any input symbol $a\in \Sigma$ and state $s\in S$, $$ G_2(s,a)=G_1(s) $$ So Mealy machines have extra functionality that Moore machines don't have. Notice in your Mealy machine diagram, for any given state every arrow coming into the state has the same output. This means that we can very easily change the output to be a function of the state, rather than of the input.

In fact, any Moore machine can be converted to a Mealy machine and vice versa, but generally the minimal Mealy machine will have fewer states than the minimal Moore machine.

For any representation of a Mealy machine, one can convert to a Moore machine without the addition or relabeling of states only if for any state of the Mealy machine, every transition into the state has the same output.

Joey Kilpatrick
  • 1,515

  • We can see by this definition that a Moore machine is just a special type of Mealy machine such that the Mealy machine's input symbol is ignored in the output.

    Do you mean that the Moore Machine's outputs first character is ignored? I don't understand the statement otherwise.

     – Arpit Saxena Nov 05 '21 at 16:22