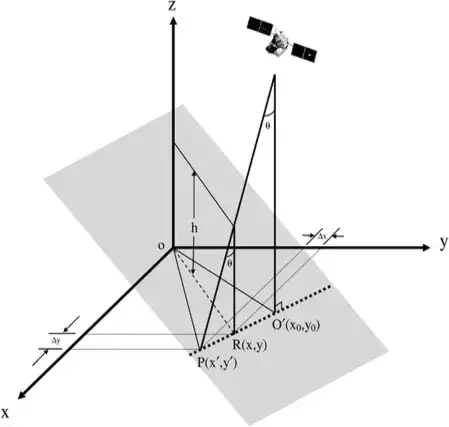
I have the above projection from this paper Projection coordinates
O'($x_0$,$y_0$) is the projection of the nadir directed vector onto the x-y plane (nadir is a technical word for direction directly below)
P(x',y') is the intersection of the off nadir incidence vector at an angle of $\theta$ with the x-y plane
R(x,y) is the projection of the off nadir incidence vector at a height h onto the x-y plane.
o(x,y,z) refers to a Cartesian coordinate system whose origin is at the center of the earth and the location of the satellite above is defined in terms of three coordinate ($\lambda$,$\phi$,R) assuming the earth to be an ellipsoid.
It is not clear to me me why $\Delta x $ should be along the y axis and $\Delta y$ should be along the x axis and also how the formula for $\Delta x $ and $\Delta y $ are arrived at.
$$ x = x' + \Delta x $$
$$ y = y' + \Delta y $$
$$\Delta x = h \tan \theta \, \, \frac {x' - x_0}{\sqrt{(x'- x_0)^2 +(y' - y_0)^2 }} $$
and
$$\Delta y = h \tan \theta \, \, \frac {y' - y_0}{\sqrt{(x'- x_0)^2 +(y' - y_0)^2 }} $$