3

I am looking for a generalization of this type of problem: Find how many integers (x,y) satisfy $$x^2+y^2\le 5$$ Obviously it's a madness to try and write them on paper (like I did). Someone gave this ideea to draw a circle and just look for points at distance of 1 (look at the picture). And it's easy to see there are 21 pairs of (x,y) that satisfying the inequality.

My questions is if we can generalize this for bigger numbers, a general formula for $$(x-a)^2+(y-b)^2\le r^2$$ or even for other geometric figures?

Zacky
  • 27,674

2 Answers2

1

First of all the number of solutions to

$$(x-a)^2+(y-b)^2\leq r^2$$

is equivalent to finding the number of solutions to

$$x^2+y^2\leq r^2$$

As the solutions are the same, just shifted by $(a,b)$ (that is, assuming they are integers). We can't find an exact solution even if $a=b=0$; mereley an approximation, and this will also more-or-less hold for non-integer $a,b$.

First, we will express $y$ in terms of $x$ and $r$. We solve $y^2+(x^2-r^2)=0$, and see that

$$y\in[-\sqrt{r^2-x^2},\sqrt{r^2-x^2}]$$

How many solutions are there for $y$ if we assume $y\in(0,\sqrt{r^2-x^2}]$ for some fixed $x\in\{0,1,\cdots r\}$ (we can simply count the positive solutions, and note we allow $x$ to be $0$, but $y\neq0$. This way we can just multiply by $4$ in the end to get the total amount of solutions). So, how many integers are there, larger than $0$, but less than or equal to $\sqrt{r^2-x^2}$? This isn't too hard; simply take the floor of $\sqrt{r^2-x^2}$. We know what range $x$ is in, so that we get

$$\sum_{x=0}^r\lfloor\sqrt{r^2-x^2}\rfloor$$

As far as I know, there's no closed formula for this; even oeis.org/A036698 doesn't know, neither does WolframAlpha. However, oeis does state

$$\sum_{x=0}^r\lfloor\sqrt{r^2-x^2}\rfloor=\tfrac14\pi r^2+O(r)$$

so that the amount of solutions in total is about $\pi r^2+O(r)$. When you think about it, that's actually not a surprise; it's like counting the amount of $1$ by $1$ squares in a circle, and that will of course be close to its area (hence $\pi r^2$).

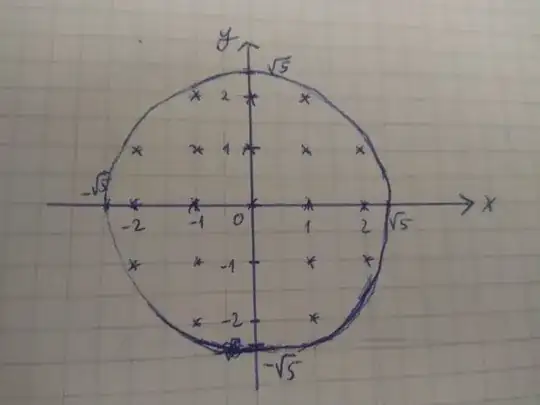
So, in your example, you got asked to solve $x^2+y^2\leq (\sqrt5)^2$. By the above, the number of solutions should be about $\pi(\sqrt5)^2\approx15.71$ while the actual solution is $21$. This seems quite far off, but once we go a little higher it becomes a better approximation; take for example $x^2+y^2\leq5^2$, where the amount of solutions is $81$ versus the estimated $\pi5^2\approx78.54$.
1

The number of pair of integers $(x , y)$ which satisfy $x^2 + y^2 \leq r^2$ can be given by $N_r = g(r) = 4 f(E(r)) + 1$, where $f$ is a function which takes $n = E(r)$ and gives the numbers of integers $(x , y)$ found in part right above of your circle (we add $1$ by the origin point). You can define $f : \mathbb{N} \to \mathbb{N}$ as $$ f(m) = \sum_{i = 0}^m h(i) \qquad \mbox{ for all } \qquad m \in \mathbb{N}\mbox{,} $$ being $h$ a function which takes a natural number $i$ between $0$ and $m$ (for fixed $m \in \mathbb{N}$) and devolves the number of natural numbers which are found in the interval $[1 , E(\sqrt{r^2 - i^2})]$ if $r > i$ and $0$ else (it is the number of pair of integers $(x , i)$, with $x \in [1 , n]$). It is $$ h(i) = \left\{ \begin{array}{lcl} \# ([1 , E(\sqrt{r^2 - i^2})] \cap \mathbb{N}) & \mbox{if} & r > i\mbox{;} \\ 0 & \mbox{if} & r \leq i\mbox{.} \end{array} \right. $$ All in all, the number of pair of integers $(x , y)$ which satisfy $x^2 + y^2 \leq r^2$ is given by $$ N_r = 1 + 4 \sum_{i = 0}^{E(r)} h(i)\mbox{.} $$ In your particular case, with the above notation, $$ h(0) = 2\mbox{, } \quad h(1) = 2 \quad \mbox{ and } \quad h(2) = 1\mbox{.} $$ Thus, $$ N = 4 (h(0) + h(1) + h(2)) + 1 = 4 \cdot 5 + 1 = 21\mbox{.} $$

joseabp91
  • 2,360