Difference between a Riemann integral and an integral against a measure

Question

Ok, this is going to be a bit abstract question:

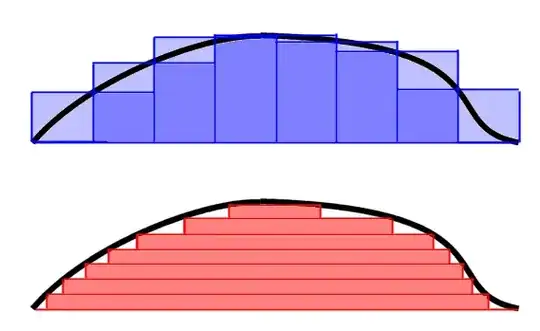
When you define the Riemann integral of a function, you first define what a step function is and you define its integral - basically the sum of the areas of the rectangles with the respective sign. Then you define the lower integral - being the supremum of the integrals of all step functions which are less than the given function, and similarly, you define the upper integral. Finally, you claim that a function is Riemann integrable if its upper integral coincides with its lower one.

When you define the Lebesgue integral (or in general, against a measure), you similarly define the set of simple non-negative functions and define their integral. But then, for a general non-negative function, you take its integral to be just the supremum of the set of all integrals of the set of non-negative functions which are less than the given one.

My question is: Why do we define the integral against a measure to involve only the supremum? Why don't we define the "upper integral" as well? Is it because of the non-negativity condition?

Answer 1

From an intuitive point of view the Riemann integral and the Lebesgue integral take two different approaches.

In the Riemann case you partition the domain into intervals, and then try to approximate the function in each interval "squashing" it between two vertical rectangles. You need two of of them to "control" the function while you make the interval small to ensure that the "variation" of the function in that interval of the domain becomes smaller as the interval shrinks.

In the Lebesgue case the situation is reversed. Now you partition the codomain of the function into intervals. For each interval $I$ in the codomain you take the inverse image $f^{-1}(I)$, which is a subset of the domain. If $f$ is measurable you are approximating it using horizontal boxes $f^{-1}(I)\times I$. You don't need to control the variation of the function, your only limitation is for $f^{-1}(I)$ to be measurable and for the process to converge.

The difference is well exemplified by comparing the two charts below where the top one is the process of approximation according to Riemann, while the second one is according to Lebesgue.