Find $\frac{dy}{dx}$ if $y=\sin^{-1}[x\sqrt{1-x}-\sqrt{x}\sqrt{1-x^2}]$, $0

Question

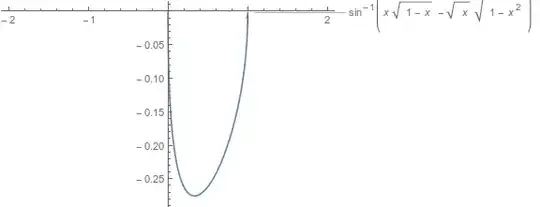
Find derivative of $f(x)=\sin^{-1}[x\sqrt{1-x}-\sqrt{x}\sqrt{1-x^2}]$, $0<x<1$

Let $x=\sin a$ and $\sqrt{x}=\cos b$

Then I'll get: $$ y=\sin^{-1}[\sin a\cos b-\cos a\sin b]=\sin^{-1}[\sin(a-b)]\\ \implies\sin y=\sin(a-b)\\ \implies y=n\pi+(-1)^n(a-b)=n\pi+(-1)^n(\sin^{-1}x-\sin^{-1}\sqrt{x}) $$ Thus, $$ y'=\frac{d}{dx}\big[n\pi+(-1)^n(a-b)\big]=\begin{cases}\frac{1}{\sqrt{1-x^2}}-\frac{1}{2\sqrt{x}\sqrt{1-x}}\text{ if }n\text{ is even}\\ -\bigg[\frac{1}{\sqrt{1-x^2}}-\frac{1}{2\sqrt{x}\sqrt{1-x}}\bigg]\text{ if }n\text{ is odd} \end{cases} $$ Is it the right way to solve this problem and how do I check the solution is correct ?

Note: I think there got to be two cases for the derivative as the graph of the function is

Answer 1

First let $g(x) = x\sqrt{1-x} + \sqrt{x}\sqrt{1-x^2}$. Then $f(x) = \sin^{-1}(g(x))$. Now we use the chain rule, so $f'(x) = \frac{1}{\sqrt{1-g(x)^2}}g'(x)$. I let you finish, by finding $g'$.

Answer 2

Use that $$(\arcsin(x))'=\frac{1}{\sqrt{1-x^2}}$$ the whole derivative is given by $$f'(x)={\frac {1}{\sqrt {- \left( x\sqrt {1-x}+\sqrt {x}\sqrt {-{x}^{2}+1} \right) ^{2}+1}} \left( \sqrt {1-x}-1/2\,{\frac {x}{\sqrt {1-x}}}+1/2 \,{\frac {\sqrt {-{x}^{2}+1}}{\sqrt {x}}}-{\frac {{x}^{3/2}}{\sqrt {-{ x}^{2}+1}}} \right) } $$ after simplifying i got: $$\frac {\sqrt {x} \left (3 x \left (\sqrt {x} + \sqrt {x + 1} \right) - 2 \sqrt {x + 1} \right) - 1} {2 \sqrt {(-x + 1) x} \sqrt {x + 1} \sqrt {2 (x - 1) \sqrt {x + 1} x^{3/2} + 2 x^3 - x^2 - x + 1}}$$

Answer 3

$$F(x)=\sin^{-1}x-\sin^{-1}\sqrt x=\sin^{-1}x+\sin^{-1}(-\sqrt x)$$

Using Proof for the formula of sum of arcsine functions $ \arcsin x + \arcsin y $,

$$\displaystyle F(x) =\begin{cases} \arcsin( x\sqrt{1-x} -\sqrt x\sqrt{1-x^2}) \;\;;x^2+x \le 1 \;\text{ or }\; x^2+x > 1, -x\sqrt x< 0\iff x>0\\ \pi - \arcsin( x\sqrt{1-x} -\sqrt x\sqrt{1-x^2}) \;\;;x^2+x > 1, 0< x,-\sqrt x \le 1\text{ which is untenable}\\ -\pi - \arcsin( x\sqrt{1-x} -\sqrt x\sqrt{1-x^2}) \;\;;x^2+x > 1, -1< x,-\sqrt x \le 0 \end{cases}$$

Answer 4

Let $\sin a=x\implies a=\sin^{-1}x$ and $\sin b=\sqrt{x}\implies b=\sin^{-1}\sqrt{x}$ $$ y=\sin^{-1}\Big[ \sin a|\cos b|-\sin b.|\cos a| \Big]\\ $$ $0<x<1\implies 0<\sin^{-1}x=a<\frac{\pi}{2}\implies |\cos a|=\cos a$ and

$0<x<1\implies 0<\sqrt{x}<1\implies0<\sin^{-1}\sqrt{x}=b<\frac{\pi}{2}\implies|\cos b|=\cos b$ $$ \begin{align} y&=\sin^{-1}\Big[\sin a\cos b-\cos a\sin b\Big]\\ &=\sin^{-1}\big[\sin(a-b)\big] \end{align} $$ We have $0<x<\frac{\pi}{2}$ and $0<b<\frac{\pi}{2}\implies \frac{-\pi}{2}<-b<0$, Hence $\frac{-\pi}{2}<a-b<\frac{\pi}{2}$ $$ y=\sin^{-1}\big[\sin(a-b)\big]=a-b=\sin^{-1}x-\sin^{-1}\sqrt{x} $$ $$ \begin{align} \color{blue}{\frac{dy}{dx}}&\color{blue}{=\frac{1}{\sqrt{1-x^2}}-\frac{1}{2\sqrt{x}\sqrt{1-x}}}\\ &=\frac{2\sqrt{x}\sqrt{1-x}-\sqrt{1-x^2}}{2\sqrt{x}\sqrt{1-x}\sqrt{1-x^2}} =\frac{\sqrt{1-x}(2\sqrt{x}-\sqrt{1+x})}{2\sqrt{x}\sqrt{1-x}\sqrt{1-x^2}} \end{align} $$ $y'<0$ when $2\sqrt{x}<\sqrt{1+x}\implies 4x<1+x\implies 0<x<\frac{1}{3}$

$y'<0$ when $\frac{1}{3}<x<1$