Shortest path between two points in a cone with a condition that the path should always be uphill.

Question

Let there be a right-circular cone with vertex O, radius$=20$ units and slant height$=60$ units. Let $A$ be a point on the base of the cone and B be a point on the line joining $OA$. Also $AB=10$ units. Find the shortest path and hence the shortest distance from $A$ to $B$ that goes around the cone with a condition that the path should always go strictly uphill.

I can solve it without that condition "strictly". I can understand that $OB<OX$ for any $X$ in the path from $A$ to $B$.

A complete solution or an idea is deeply appreciated.

Answer 1

If the condition were merely that the path cannot go downhill, to find the shortest path you could unroll the cone to a circular wedge with radius $60$ and vertex angle $\frac23\pi.$ The shortest path would run along a straight segment from one end of the radius-$60$ arc to a tangent point on a concentric arc of radius $50$ and then follow the radius-$50$ arc to the other end. If $L$ is the length of this path, then $$L=\sqrt{60^2-50^2} + 50\left(\frac23\pi - \arccos\frac56\right).$$

Here's a rough sketch of the unrolled cone and the key features of the shortest never-downhill path:

Angle $\angle AOB = \frac23\pi,$ angle $\angle AOT = \arccos\frac56,$ the line $AT$ is tangent to the arc $BT$ at $T,$ and the path consists of the segment $AT$ and the arc $BT.$

Intuitively, since we can never get closer than distance $50$ from $O$ (since otherwise we'd have to go downhill to get to $B$), the path is constrained to the region between the two arcs. If we imagine running a string from $A$ to $B$ and then pull the string as tight as possible, all while staying within that region, the string will follow the path shown.

Any other path that goes around the cone from $A$ to $B$ will either go downhill at some point or will be longer than $L.$ But you can construct a path that is uphill everywhere and whose length is as close to $L$ as you want simply by replacing the arc of radius $50$ by a suitable spiral. For example, construct a spiral path from $B$ to a point $C$ on $OA$ such that $OC = 50.000001,$ then construct a line through $A$ tangent to that spiral at a point $T'$; the path is the segment $AT'$ plus the part of the spiral from $T'$ to $B,$ all of it strictly uphill. To make an even shorter path, set $OC = 50.000000001$ instead of $50.000001.$ The only limit on how short you can make this path is that if you reduce $OC$ to $50$ exactly, then you have a path of exactly length $L,$ but then the path is not strictly uphill the whole way.

Hence the number you are seeking, the length of the shortest uphill path around the cone from $A$ to $B,$ is the smallest number greater than $L.$

Answer 2

I think there is no shortest path fulfilling the "strictly uphill" condition. Its like finding the smallest positive number. I suggest you replace the "strictly uphill" with "never downhill", and then you have a shortest path of the required kind.

To put it differently: In order to guarantee that there is an optimal feasible solution the set ${\cal L}$ of feasible solutions should in some way be compact. A condition like "strictly uphill", meaning that $z'(t)>0$ for all $t\in[0,1]$, does not make for a compact ${\cal L}$.

Answer 3

When cone is cut along cone generator $OA$ and laid out flat on development, we have a sector as follows. Highest point to A length $ 10.$ Slant generator length at $B$ from Pythagoras relation is:

$$ sl = \sqrt {60^2 -10^2 } = 59.16$$

AB is the shortest path geodesic. At $B$ the tangent is horizontal and is parallel to ground (base circle) plane.

A to B is uphill path. Instantaneosly at B the path is having horozontal slope. A on other side to old B is downhill. B is the highest point touched shown in the development below.

Answer 4

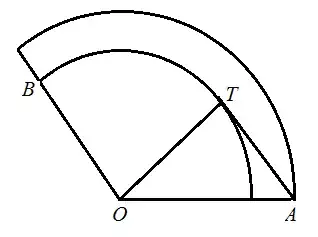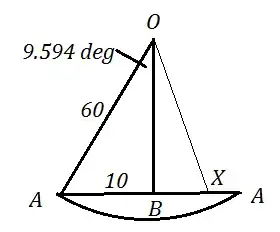
A solution can be derived by using a development (opened out cone along the slant line ABO) of the cone basis the following constraints:

1. All points on the curve connecting A & B should be between the base circle to the cone at point A & point B.
2. The slope of the curve on all points should be positive, i.e., increasing

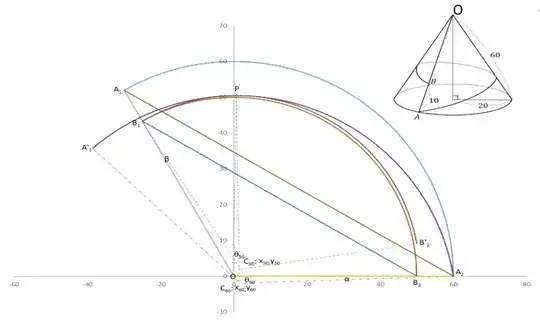
Cone development will be an arc of radius 60 and and angle 120° at arc center. Basis the above, one potential solution can be derived by rotating arc $A_1A_2$ (radius 60) counterclockwise along vertex $A_2$, rotating arc $B_1B_2$(radius 50) counterclockwise along $B_1$, finding intersection point of arc $A_1A_2$ and $B_1B_2$, such that the slope of the curve at the point of intersection is zero or horizontal. Then the total length of the path will be sum of arclength $A_2P$ and $PB_1$. Assuming that arc $A_1A_2$ and $B_1B_2$ are rotated by angle $\alpha$ and $\beta$ respectively, then the co-ordinates for the new location of their centers $C_{60}$ and $C_{50}$ will be given by: $$X_{60} = 60(1 - \cos(360°-\alpha))$$ $$Y_{60} = 60\sin(360° - \alpha)$$ $$X_{50} = 50(\sin(30° + \beta) - \sin30°$$ $$Y_{50} = 50(\cos30°- \cos(30°+\beta))$$

Any point on the arc $A_2A^{'}_1$ and $B_1B^{'}_2$ will be governed by the relation : $$Y_A = Y_{60} + \sqrt{60^2 - (X_A - X_{60})^2}$$ $$Y_B = Y_{50} + \sqrt{50^2 - (X_B - X_{50})^2}$$

For the slope of the arcs at the point of intersection to be zero, the derivatives of $Y_A$ and $Y_B$ would be zero: $$\therefore \frac{d}{dx}Y_A = 0\quad and \quad \frac{d}{dx}Y_B = 0$$

$$\therefore -\frac{X_A - 60(\cos(360°-\alpha))}{\sqrt{60^2 -(X_A - 60(1 - \cos(360°-\alpha)))^2}} = 0$$ and $$-\frac{X_B - 50(\sin(30+\beta)-\sin30°)}{\sqrt{50^2 - (X_B - 50(\sin(30°+\beta) - \sin30°))^2}} = 0$$ Solving the above two equations, gives the 'X' co-ordinate for the point of intersection as: $$X_A = 60(1-\cos(360°-\alpha)) = X_{60}$$ and $$ X_B = 50(\sin(30°+\beta) - \sin30°) = X_{50}$$ Substituting above $X_A$ and $X_B$ values in equations for $Y_A$ and $Y_B$ above, gives: $$Y_A = 60(1+\sin(360°-\alpha))$$ and $$Y_B = 50(\cos30° - \cos(30°+\beta) + 1)$$ Now as these are the co-ordinates for the point of intersection of the arcs: $$\therefore X_A = X_B\quad and \quad Y_A = Y_B$$ Solving for $\alpha$ and $\beta$, gives: $$\alpha = 9.158°\, and\; \beta = 1.017°$$ Now as the X co-ordinates for both arc centers and the point of intersection are the same, arc centers and point of intersection are on a single straight line parallel to Y-axis. Hence:

Angle of arc $A_2P$ at its center $= 90°-\alpha = 90°-9.158° = 80.842° = 1.41096$ radians

Angle of arc $PB_1$ at its center $= 30°+\beta = 30°+1.017° = 31.017° = 0.54135$ radians

Hence, the total distance from A to B around the cone:

$=$ Arclength $A_2P +$ Arclength $PB_1$
$=A_1A_2$ arc radius $\times$ Arc angle $+\;B_1B_2$ arc radius $\times$ Arc angle $=60\;\times\;1.41096\;+50\;\times\;0.54135=111.725$