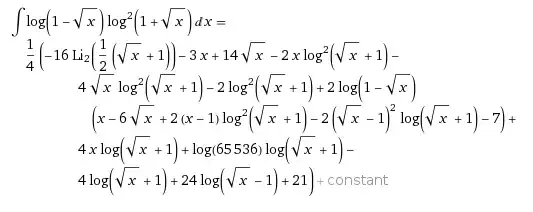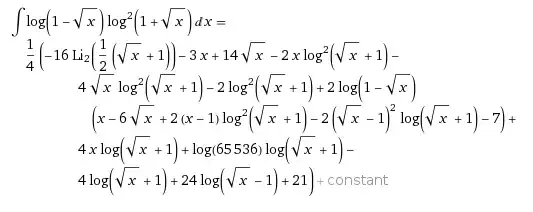How do I evaluate this integral $$\int_{0}^{1}\mathrm dx\ln^2(1+\sqrt{x})\ln(1-\sqrt{x})?$$
Enforcing $x=\tan^2(y)$
$$\int_{0}^{\pi/4}\mathrm dy\sec^2y\tan y\ln^2(1+\tan y)\ln(1-\tan y)$$
Enforcing $v=1+\tan y$
$$\int_{1}^{1+\pi/4}\mathrm dv (v-1)\ln^2(v)\ln(2-v)\tag1$$
$$(1)=\int_{1}^{1+\pi/4} v\ln^2(v)\ln(2-v)\mathrm dv-\int_{1}^{1+\pi/4} \ln^2(v)\ln(2-v)\mathrm dv$$
MY "ANSWER": I can get you started on the right track using the following two identities:
$$\bbox[lightgray,15px] { \int_0^1 x^n\ln(1-x)dx=-\frac{H_{n+1}}{n+1} }$$
$$\bbox[lightgray,15px] { \frac{1}{2}\ln^2(1-x)=\sum_{n=1}^\infty \frac{H_n x^{n+1}}{n+1} }$$
From these, we have $$\begin{align} \int_0^1 \ln(1-\sqrt x)\ln^2(1+\sqrt x) &=\int_0^1 2x\ln(1-x)\ln^2(1+x)dx\\ &=\int_0^1 4x\ln(1-x)\sum_{n=1}^\infty \frac{(-1)^{n+1}H_n x^{n+1}}{n+1}dx\\ &=4\sum_{n=1}^\infty \frac{(-1)^{n+1}H_n}{n+1}\int_0^1 x^{n+2}\ln(1-x)dx\\ &=4\sum_{n=1}^\infty \frac{(-1)^{n}H_n}{n+1}\frac{H_{n+3}}{n+3}\\ &=4\sum_{n=1}^\infty \frac{(-1)^{n}H_nH_{n+3}}{(n+1)(n+3)} \end{align}$$
This is an Euler Sum and can probably be computed using some polylogarithms and a lot of algebra. Euler sums get really messy to do by hand, so this is where I abandon the problem and turn to Wolfram.
WOLFRAM'S ANSWER: Wolfram evaluates this integral as
$$\int_0^1 \ln(1-\sqrt x)\ln^2(1+\sqrt x)=\frac{11}{4}-\frac{\pi^2}{3}$$
and actually gives an antiderivative:
We are interested in $$\mathcal{J}= \int_{0}^{1}2x\log^2(1+x)\log(1-x)\,dx$$ and by integration by parts this boils down to computing $$ \int_{0}^{1}(1+x)\log^2(1+x)\,dx = \frac{3}{4}+2\log^2(2)-2\log(2)$$ $$ \mathcal{K} = \int_{0}^{1}(1-x)\log(1-x)\log(1+x)\,dx$$ and $\mathcal{K}$ can be tackled by enforcing the substitution $x=\cos\theta$ and by exploiting the Fourier series of $\log\sin$ and $\log \cos$. TLDR: an initial step of integration by parts allows to reduce $\mathcal{J}$ from an (alternating) Euler sum with weight $4$ to some Euler sums with weigth $\leq 3$, which are way more manageable. The final outcome is $\mathcal{J}=\frac{11}{4}-2\,\zeta(2)$. We may also integrate by parts twice to reduce the problem to the computation of $$ \mathcal{I}_\pm = \int_{0}^{1}(1-x)^2\frac{\log(1\pm x)}{1\mp x}\,dx $$ which is fairly simple (Euler sums with weigth $\leq 2$).
