2

The distribution is $R^2\sim \exp(\lambda)$ and I want to find the pdf(R). Here is what I did.

Let $$Y=R^2$$ Then $$P(R \le r)=P(\pm \sqrt{Y} \le r)=P(-r\le\sqrt{Y}\le r)$$

At this point, the probability would cancel out. I am not sure if I am on the right track. Any tips would be greatly appreciated!

hellowurf
  • 35
  • Can $R$ be negative and/or positive? – Mostafa Ayaz Apr 20 '18 at 21:02
  • 1
    There is no unique distribution for $R$ unless you impose some constraints, like "$R$ is positive" or "$R$ has a symmetric distribution over the reals." – angryavian Apr 20 '18 at 21:03
  • 1
    Related but you have to say $R=\sqrt{Y}$ instead: https://math.stackexchange.com/questions/1512756/ https://math.stackexchange.com/questions/1512756 https://math.stackexchange.com/questions/678491 http://www.math.wm.edu/~leemis/chart/UDR/PDFs/ExponentialRayleigh.pdf – BCLC Apr 20 '18 at 21:26
  • 1
    @angryavian I had a feeling about that. But I wasn't too sure. From the looks of it, it is positive. – hellowurf Apr 21 '18 at 03:10

3 Answers3

2

For $R \ge 0$

$$P(R \le r)=P(\sqrt{Y} \le r)=P(Y \le r^2) = 1 - \exp(-\lambda r^2)$$

See Rayleigh distribution.

In general,

$$1 - \exp(-\lambda y) = P(Y \le y) = P(R^2 \le y)=P(-\sqrt{y} \le R \le \sqrt{y}) = F_R(\sqrt{y}) - F_R(-\sqrt{y})$$

If R has a pdf, then

$$\int_{-\infty}^{\sqrt{y}} f_R(s) ds - \int_{-\infty}^{\sqrt{-y}} f_R(s) ds$$

BCLC
  • 13,459
2

Let $R\ge0$. Therefore $$\Pr(R<r){=\Pr(R^2<r^2)\\=1-e^{-\lambda r^2}\\=F_R(r)\to \\f_R(x)=2x\lambda e^{-\lambda x^2}}.$$

BruceET
  • 51,500
Mostafa Ayaz
  • 31,924
1

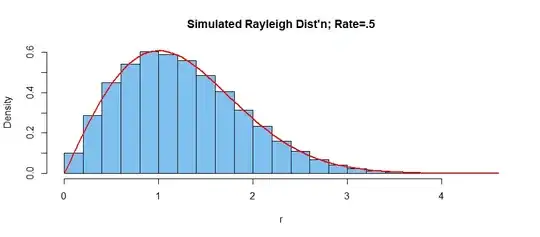
Comment: Using R to sample $n=100,000$ observations from $\mathsf{Exp}(rate = .5)$ in order to illustrate @MostafaAyaz's (+1) Rayleigh density function [red curve].

y = rexp(10^5, .5);  r = sqrt(y)
hist(r, prob=T, col="skyblue2", main="Simulated Rayleigh Dist'n; Rate=.5")
curve(2*x*.5*exp(-.5*x^2), add=T, lwd=2, col="red")

enter image description here

Note: The Rayleigh distribution has practical uses. One of them occurs in the 'Box-Muller transformation' to generate standard two normal random variables from two uniform random variables. If interested, you can look at Wikipedia pages on 'Rayleigh distribution' and 'Box-Muller transformation' for more information.

BruceET
  • 51,500