Let $f:(0,1)^2\to\mathbb R$ be, as in the question, separately continuous in each variable. Let $\omega_f$ be the oscillation function of $f$. The set of points of full continuity of $f$ is precisely $\{p\mid\omega_f(p)=0\}$, which is the intersection of $O_\epsilon=\{p\mid\omega_f(p)< \epsilon\}$ for $\epsilon=1, \frac12,\frac13$... These sets are open with absolutely no assumptions on $f$, because the oscillation of a function is always upper semicontinuous. If we can show they're also dense, then by Baire's theorem we'll obtain that the set of points of continuity of $f$ is dense in its domain.
Suppose $O_\epsilon$ were not dense. Then there would be some open set $U$ disjoint from it. What it means for $U$ to be disjoint from $O_\epsilon$ is that for every point $p\in U$, there is a sequence of points $p_n\to p$ such that $|f(p_n)-f(p)|>\epsilon$. Of course these points cannot be horizontally or vertically aligned with $p$, as this would contradict the separate continuity of $f$. However, what we can show is:
Claim. In any open set $U$ disjoint from $O_\epsilon$, there exists a pair of vertically aligned points $p_1$, $p_2$ with $|f(p_1)-f(p_2)|>\frac \epsilon 2$.
Proof of claim. Take some point $p\in U$. Take some point $p_1$ such that $|f(p)-f(p_1)|>\epsilon$, and let $p_2$ be its orthogonal projection onto the horizontal axis through $p$. Take $p_1$ sufficiently close to $p$ so that $|f(p)-f(p_2)|<\frac \epsilon 2$ - this is always possible by horizontal continuity of $f$. Since $|f(p)-f(p_2)|+|f(p_1)-f(p_2)|\geq|f(p)-f(p_1)|>\epsilon$, we must have $|f(p_1)-f(p_2)|>\frac \epsilon 2$, and $p_1$ and $p_2$ are vertically aligned. $\blacksquare$
If two points $a$ and $b$ satisfy $|f(a)-f(b)|>k$, I'll say they're of $k$-variation.
Now, we're going to use this construction to obtain a contradiction out of the existence of $U$. Here's what we're going to do. We're going to build a sequence of pairs of points $a_1, a_2; b_1, b_2; c_1, c_2$... such that for some constant $k>0$, each pair is of $k$-variation. We'll construct these points to be vertically aligned, and such that they converge onto a single limit point. This will contradict the vertical continuity of $f$.
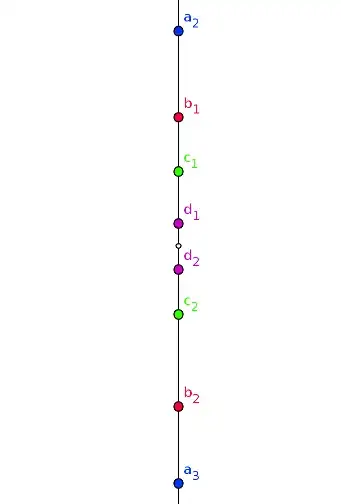
We will not pick the axis on which these points are to be aligned in advance. What we'll do is construct a sequence of pairs of points $a_1, a_2; b_1, b_2; c_1, c_2$... such that each pair is of $\frac\epsilon2$-variation, and each pair is vertically aligned, but distinct pairs are not necessarily vertically aligned. Now, every point in the plane has a small horizontal segment centered on it such that $f$ varies by less than $\frac \epsilon {8}$ on that segment. We will construct our points such that all of their horizontal segments overlap, that is, their projections onto the $x$-axis have non-empty intersection. This guarantees that a vertical line exists which intersects all of these horizontal segments. Those points of intersection will be our convergent sequence of vertically aligned points promised in the previous paragraph (you will see in the construction why they're guaranteed to converge). These pairs are, as required, of $k$-variation for some $k>0$, since if $a_1',a_2'$ are the projections of $a_1, a_2$, we have $|f(a_1')-f(a_2')|\geq|f(a_1)-f(a_2)|-2\frac{\epsilon}{8}\geq\frac\epsilon4$.
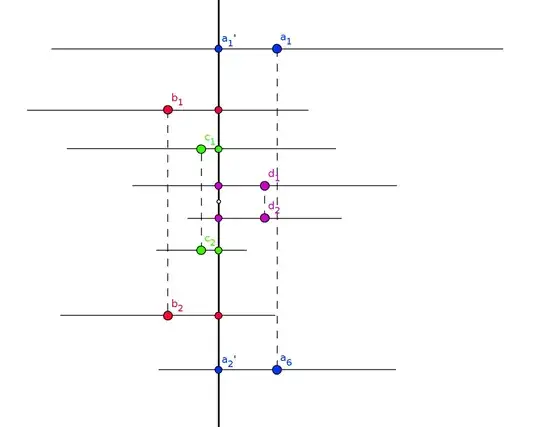
So, let's kick things off by picking some pair of vertically aligned points $a_1, a_2$ of $\frac\epsilon2$-variation. Consider the two horizontal segments centered at these points on which $f$ varies by at most $\frac \epsilon 8$. One of those segments is shorter, consider the open rectangle $R$ having it as its base, sandwiched between the two segments. We can guarantee $R\subseteq U$ by picking $a_1, a_2$ from a smaller open subset of $U$, and making $R$ a little thinner, if necessary.
Now, inside $R$, pick the next two points $b_1$, $b_2$ of $\frac\epsilon2$-variation. Construct another rectangle $R'$ from these points in the same way, and in addition take its intersection with $R$ to get a smaller rectangle nested in $R$, if necessary. We can continue in this way, creating nested rectangles and pairs of points, forever. We will always be able to find a pair of points in each rectangle, because our above Claim works for any open set disjoint form $O_\epsilon$, which each of those rectangles is. As was promised, the horizontal segments of small variation of $f$ are all overlapping.
You may have noticed that nothing in our construction guarantees that the vertical projections of our points onto the aforementioned vertical line will converge. In order to force this situation, all we have to do is make our nested rectangles of heights converging to zero. Thus if $R_n$ is the $n$-th rectangle in our construction, shorten to a height of $\frac 1 n$ if necessary before continuing. Our sequence of pairs of points is now contained in a nested sequence of rectangles whose heights tend to zero, so the vertical projections are a Cauchy sequence.

