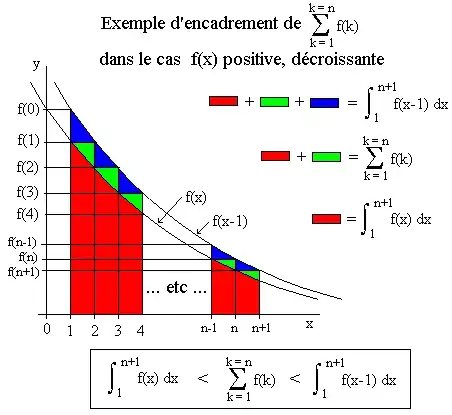
$\sum_{k=1}^{n} \frac{1}{n+k} < \ln 2$
Here are some proofs for this inequality but I have another approach. Can anyone verify my proof? Thanks.
$$\sum_{k=1}^{n} \frac{1}{n+k}< \int_0^n \frac{1}{n+x}dx=\ln (n+x)\mid ^n_0 = \ln(2n)-\ln(n) = \ln 2.$$
Does the first inequality of this proof hold? In general, what's the relationship between a series and its integral form? Is the series always less than its integral form? Is it the same for a finite summation?