Let $AB′C$ be a triangle with $\angle B′AC = 70^\circ$, $\angle ACB′ = 80^\circ$, $F$ is a point inside the triangle such that $\angle FB′A = \angle FCB` = 20^\circ$. Find $\angle AFB′$.
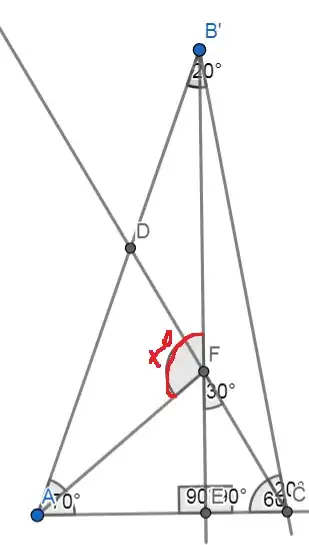
Let $AB′C$ be a triangle with $\angle B′AC = 70^\circ$, $\angle ACB′ = 80^\circ$, $F$ is a point inside the triangle such that $\angle FB′A = \angle FCB` = 20^\circ$. Find $\angle AFB′$.

Denote $h = EB'$, $a=EF$. Then $$EC = h\tan 10^{\circ},\quad AE = h\tan20^{\circ};$$ and other side: $$EC = a\tan 30^{\circ},\quad AE = a\tan x,$$ where $x=\angle AFE$; so $$h\tan 10^{\circ}=a\tan 30^{\circ}, \quad h\tan20^{\circ}=a\tan x;$$ therefore $$\tan x = \dfrac{h}{a}\tan 20^{\circ} = \dfrac{\tan 30^{\circ}}{\tan 10^{\circ}}\cdot \tan 20^{\circ}.$$
It remains to show that $x=50^{\circ}$ and so $\angle AFB' = 180^{\circ}-x=130^{\circ}$.
To see that $$\dfrac{\tan 20^{\circ} \tan 30^{\circ}}{\tan 10^{\circ}} = \tan 50^{\circ},$$ you can review this question+answers.