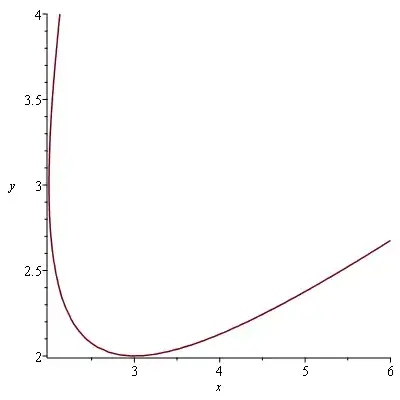
View the curve $ \ (y-x)^2+2=xy-3 \ $ as a contour of $ \ f(x,y) \ $
Use $ \ \nabla f(3,2) \ $ to find a vector normal to the curve at $ \ (3,2)\ $
Answer:
Let $ \ f(x,y)=(y-x)^2-xy+5=0 \ $
Then,
$ \nabla f(x,y)=\left\langle f_x,f_y \right\rangle \ = \left\langle 2(x-y)-y,2(y-x)-x \right\rangle $
Therefore,
$ \nabla f(3,2)=\left\langle0,-5 \right\rangle \ $ , which is normal t the level curves but not on the curve $ \ f(x,y) \ $
How to find find the vector normal to the curve $ \ f(x,y) \ $ using $ \ \nabla f(3,2) \ $ ?
Help me doing this.