Right continuous and monotone function must exist right derivative?
Suppose $f:R\rightarrow R$ is a right continuous and monotone function, i.e. $f(x+)=f(x),\forall x\in R$ and $f(x)$ is monotone, say non-decreasing. Does the limit exist $\lim_{\delta \searrow 0 }\frac{f(x+\delta)-f(x)}{\delta}$ everywhere ?
No, a simple counterexample is $\sqrt x$. Another is $x+\sqrt{\max(0,x-1)}$.
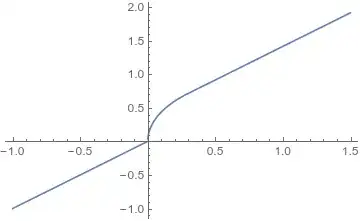
$$f(x) = \begin{cases}
x &, x<0 \\
\sqrt{2x - x^2} &, 0 \leq x < \frac{1}{2}(2-\sqrt{2}) \\
x - 1 + \sqrt{2}&, \frac{1}{2}(2-\sqrt{2}) \leq x
\end{cases}$$
is continuous everywhere, strictly monotonically increasing everywhere, and (two-sided) differentiable on $\mathbb{R} \smallsetminus\{0\}$. At $x = 0$, the left derivative is $1$ and the right derivative is undefined.
What kinds of discontinuities (in $f'$) are there? Removable, infinite, jump,
endpoint, essential, and mixed (like $\mathrm{e}^{1/x}$). Which of these can we make work? Yves Daoust makes an infinite endpoint discontinuity with $\sqrt{x}$. I made a mixed discontinuity above. Essential singularities can be made to work. (Glue $\int_{-1}^x 1+\sin(1/u) \, \mathrm{d}u$ on $(-\infty,0)$ to $2 - \int_{x}^1 1+\sin(1/u) \, \mathrm{d}u$ on $(0,\infty)$ along $\left( 0,\frac{1}{2} \right)$.) Infinite discontinuity is easy: glue two quarter circles together (or any other endpoint-like discontinuities).
Jump isn't strong enough, since you only need a one-sided derivative. Removable isn't strong enough either. (What would a Calculus student do with $\frac{\mathrm{d}}{\mathrm{d}x} \frac{x^2}{x}$, starting with either the quotient rule or the definition of the derivative? We allow cancellation under the limit sign that extends the domain of the resulting expressions. Of course, we remember that the derivative is undefined when the function is undefined...)
Any time you think that continuity might imply something about differentiability, the Cantor function is usually a counterexample.
It's continuous and monotone increasing. But you can check directly that $f(3^{-n}) = 2^{-n}$. So taking $x=0$ and $\delta = 3^{-n}$, so that $\delta \to 0$ as $n \to \infty$, your difference quotient equals $(2/3)^{-n}$ which blows up as $n \to \infty$. Indeed this function is non-right-differentiable at any point of the Cantor set which is not a "right endpoint".
You can say, however, that every continuous monotone increasing function is (two-sided) differentiable almost everywhere. See Monotone+continuous but not differentiable.
