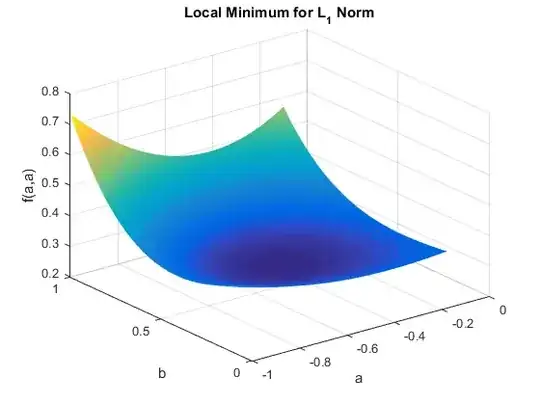
Starting from Ian's comment, the roots of $e^x-a-b x=0$ are given by
$$r_1=-W_0\left(c\right)-\frac{a}{b}\qquad \text{and} \qquad r_2=-W_{-1}\left(c\right)-\frac{a}{b}\qquad \text{with} \qquad c=-\frac{1}{b}e^{-\frac{a}{b}}$$ Computing the three integrals as suggested by Ian, we end, for
$$\| f\|_1 = \int_{-1}^1 |e^x-a-b\,x|\,dx$$ to the quite unpleasant expression
$$\| f\|_1 =b
\left(W_0\left(c\right)-W_{-1}\left(c\right)\right)
\left(W_0\left(c\right)+W_{-1}\left(c\right)+2\right)+2 a-e+\frac{1}{e}$$ but the partial derivatives are not "too" bad
$$\frac{\partial \| f\|_1}{\partial a}=-2 W_0\left(c\right)+2
W_{-1}\left(c\right)+2\tag 1$$
$$\frac{\partial \| f\|_1}{\partial b}=\frac{\left(W_0\left(c\right)-W_{-1}\left(c\right)\right) \left(b
\left(W_0\left(c\right)+W_{-1}\left(c\right)\right)+2 a\right)}{b}\tag 2$$
Using as estimates
$$a=\frac{e^2-1}{2 e}=\sinh(1)\qquad \text{and} \qquad b=\frac 3 e$$ which are the solutions of the minimization of
$$\int_{-1}^1 (e^x-a-b\,x)^2\,dx$$ we can easily solve $(1)$ for $c$ starting iterating from $c_0=-\frac{1}{3} e^{\frac{7-e^2}{6}}$ and get the following iterates
$$\left(
\begin{array}{cc}
k & c_k \\
0 & -0.312404963823450 \\
1 & -0.325786585779692 \\
2 & -0.325205861061641 \\
3 & -0.325204338150736 \\
4 & -0.325204338140427
\end{array}
\right)$$
Then, from $(2)$, $b=-\frac {2a}{W_0\left(c\right)+W_{-1}\left(c\right) }$ and, back to the definition of $c$, get $a$. All of that leads to
$$a=1.1276259652064\qquad \text{and}\qquad b=1.0421906109875$$ which, to my surprise, are recognized by inverse symbolic calculators
$$\color{blue}{a=\frac{1+e}{2 \sqrt{e}}=\cosh \left(\frac{1}{2}\right)}\qquad \text{and} \qquad \color{blue}{b=\frac{e-1}{ \sqrt{e}}=2 \sinh \left(\frac{1}{2}\right)}$$
Update
The results could have obtained analytically since, looking here
$$W_0(c)-W_{-1}(c)=1 \implies c=-\frac {1} {e-1}\, \exp \left( \frac {-1} {e-1}\right)$$ is known result which makes
$$W_0(c)=\frac{1}{1-e} \qquad \text{and} \qquad W_{-1}(c)=\frac{e}{1-e}$$ Then, from $(2)$
$$b=-\frac{2a} {W_0(c)+ W_{-1}(c)}=\frac{2 (e-1) }{1+e}a$$ and reusing the definition of $c$, then $a$ and $b$. QED.