Shortest Distance Around Cone

Question

An ant wants to get from (0,-2) to (0,2). However, there is a cone of radius 1 and height h at (0,0). What is the length of the shortest route?

Going around the cone uses $\frac{\pi}{3}+2\cdot \sqrt{3} ≈ 4.5$;

Going straight over takes $2+2\cdot \sqrt{h^2+1}$

Walking on side of cone might be shorter, but I cannot visualize it.

Answer 1

Let us consider the path from $(0,-2, 0)$, straight to some point of the basis of the cone, let $(\cos\alpha,-\sin\alpha, 0)$, then following the geodesic to the symmetrical point $(\cos\alpha,\sin\alpha, 0)$ and then straight to $(0,2,0)$.

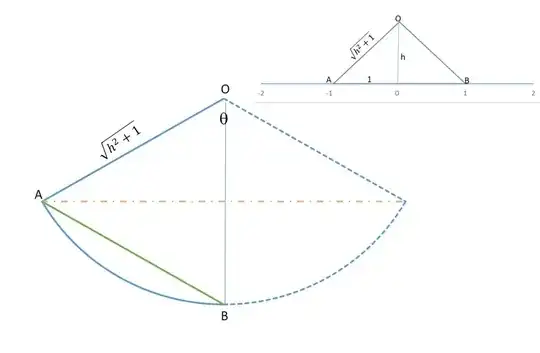
Following this answer (https://math.stackexchange.com/a/2061892/65203), when you flatten the cone, the geodesic is simply a chord of the circumference of radius $a:=\sqrt{1+h^2}$. As the arc along that circumference has length $2\alpha$, this corresponds to an aperture angle of $\dfrac{2\alpha}a$, and the chord length is given by $2a\sin\dfrac\alpha a$.

Hence the total path length is

$$2\sqrt{\cos^2\alpha+(2-\sin\alpha)^2}+2a\sin\frac\alpha a$$ which you need to minimize for $\alpha\in[\frac\pi6,\frac\pi2]$.

As this function is increasing in the given range, the minimum is always achieved for $\alpha=\frac\pi6$, giving the minimum length

$$2\sqrt3+2a\sin\frac{\pi}{6a}.$$

---

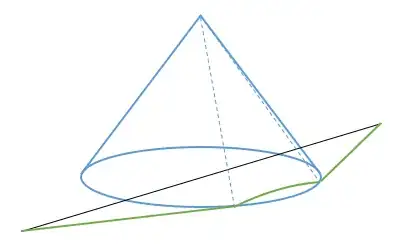
Update:

I wrongly stated that the function is increasing. This is not true for small values of $a$. Then the problem requires the resolution of a nasty nonlinear equation.

Answer 2

My simple thought runs like this. The shortest distance between two points is always a straight line. Hence taking a development (opening out) of the cone, which will be an sector of radius $\sqrt{h^2+1}$ and included angle at center equal to $\theta = \frac{2\pi}{\sqrt{h^2+1}}$ , the straight line on the surface of the cone from pt $A(0, -1)$ to $B(0, 1)$ will be a chord of length $$\overline {AB} = \sqrt{2(h^2 + 1)\left(1- \cos\left(\frac{\pi}{\sqrt{h^2+1}}\right)\right)}$$ Angle are in radians. Hence, shortest distance would be: $$2 + \overline {AB}$$ Equations used in above are:

1. Circumference of a circle $= 2\times\pi\times$ radius of circle (for finding arc length $=2\times\pi\times$ base circle radius)
2. Arc length $=$ radius of Arc $\times$ included angle at arc center (for angle $\theta =\frac {Arc\; length}{Arc\;radius}=\frac{2\pi}{\sqrt{h^2+1}}$, angle in radians)
3. Given sides a, b and included angle $\theta$, in a triangle, third side, $c^2 = a^2 + b^2 - 2ab\cos\theta$.

Answer 3

If the cone were instead a cylinder, the shortest path from a given point on the surface to the point diametrically opposite would evidently be along the circle through that point parallel to the cylinder's base.

For a cone, however, some physical considerations might be helpful. Suppose we pin a rubber band to the starting point and stretch it over a physical model of the cone to the opposite point on the cone's base.

Assuming for simplicity a right cone, the rubber band will contract until it lies on the ellipse whose major axis is perpendicular to the line between start and finish points and to the side of the axial triangle perpendicular to that line. In the figure, starting point $D$ and opposite point $E$ on the cone's base are joined by $DE$ perpendicular to the major axis $HG$ which is perpendicular to side $BC$ of axial triangle $ABC$ to which $DE$ is perpendicular. Since $G$ is the point on $BC$ closest to the center $F$ of the cone's base, the portion $DGE$ of an ellipse will be the shortest path on the cone from $D$ to $E$.

This is not a fully mathematical argument, and I have not done this rubber band experiment on physical cones. But I have some experience trying to mend broken terra cotta pots by twist-tightening wires, and this analysis of the ant problem is in line with that experience.

The specifics of the ellipse should not be difficult to determine from the givens of the problem.