2

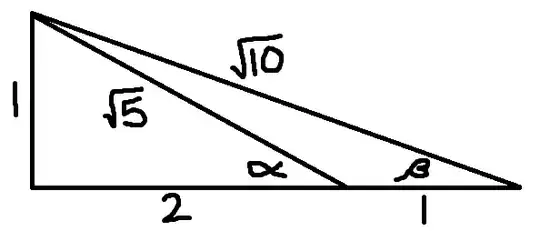
Evaluate: $$\operatorname{arccos} \frac{2}{\sqrt5} + \operatorname{arccos} \frac{3}{\sqrt{10}}$$

We let $$\alpha = \operatorname{arccos} \frac{2}{\sqrt5} \qquad \beta = \operatorname{arccos}\frac{3}{\sqrt{10}}$$

Then we have:

$$\begin{align} \cos(\alpha) = \frac{2}{\sqrt5} &\qquad \cos(\beta) = \frac{3}{\sqrt{10}} \\[4pt] \sin(\alpha) = \frac{1}{\sqrt5} &\qquad \sin(\beta) = \frac{1}{\sqrt{10}} \end{align}$$

In order to evaluate, we are told, we first determine $\sin(\alpha + \beta)$; we wind up with $1/\sqrt2$, thus we have $\pi/4$.

What I am confused about is why we have to use sin($\alpha + \beta$). For example, if I were to use $\cos(\alpha + \beta)$, I would get the answer $7/(\sqrt{10}\sqrt5)$, which I do not know what to do with. I am having trouble finding out whether there is some kind of pattern to this kind of thing, or did the author just know to use $\sin(\alpha + \beta)$ since he/she checked cos and saw nothing comes out of this?

Any help is much appreciated, thank you

Blue
  • 75,673
Algebra 8
  • 61

4 Answers4

2

As an alternative approach (which, truthfully, arose from my not reading your question carefully and, essentially, wishing to draw in MS Paint) see the following diagram in which the expression you wish to evaluate is the angle sum $\alpha + \beta$:

enter image description here

Next, let us consider instead $\tan(\alpha + \beta)$ using a tangent identity:

$$\tan(\alpha + \beta) = \frac{\tan\alpha + \tan\beta}{1 - \tan\alpha \tan\beta} = \frac{1/2 + 1/3}{1 - (1/2)(1/3)} = \frac{5/6}{5/6} = 1$$

Observe $\alpha + \beta \in (0, \pi)$; the unique angle in this interval yielding a tangent of $1$ is $\pi/4$.

Benjamin Dickman
  • 14,451
0

From $\sin(\alpha+\beta)=\frac1{\sqrt2}$, we should expect $|\cos(\alpha+\beta)|=\frac1{\sqrt2}$ from the formula $\sin^2 \theta + \cos^2 \theta = 1$.

\begin{align} \cos(\alpha+\beta)&=\cos(\alpha)\cos(\beta)\color{blue}-\sin(\alpha)\sin(\beta)\\ &=\frac{2}{\sqrt5}\cdot \frac{3}{\sqrt{10}}-\frac1{\sqrt5}\cdot \frac{1}{\sqrt{10}}\\ &=\frac{6}{5\sqrt{2}}-\frac{1}{5\sqrt2}\\ &=\frac{5}{5\sqrt2}\\ &=\frac{1}{\sqrt2} \end{align}

Siong Thye Goh
  • 149,520
  • 20
  • 88
  • 149
0

You can directly use the formula $$\cos^{-1}x+\cos^{-1}y=\cos^{-1}(xy-\sqrt{1-x^2}\sqrt{1-y^2})$$ $$x=\frac{2}{\sqrt{5}},y=\frac{3}{\sqrt{10}}$$ $$=\cos^{-1}\left(\left(\frac{2}{\sqrt{5}}\right)\left(\frac{3}{\sqrt{10}}\right)-\sqrt{1-\left(\frac{2}{\sqrt{5}}\right)^2}\sqrt{1-\left(\frac{3}{\sqrt{10}}\right)^2}\right)$$ $$=\cos^{-1}\left(\frac{6}{\sqrt{50}}-\sqrt{1-\frac45}\sqrt{1-\frac{9}{10}}\right)$$ $$=\cos^{-1}\left(\frac{6}{\sqrt{50}}-\sqrt{\frac15}\sqrt{\frac{1}{10}}\right)$$ $$=\cos^{-1}\left(\frac{6}{\sqrt{50}}-\frac{1}{\sqrt{50}}\right)$$ $$=\cos^{-1}\left(\frac{5}{\sqrt{50}}\right)$$ $$\cos^{-1}\frac{2}{\sqrt{5}}+\cos^{-1}\frac{3}{\sqrt{10}}=\cos^{-1}\left(\frac{5}{\sqrt{50}}\right)$$

Key Flex
  • 9,475
  • 7
  • 17
  • 34
  • Thank you all very much, I am studying for the GRE and the author gave the formula cos($\alpha + \beta$) = cos$\alpha$cos$\beta$ + sin$\alpha$sin$\beta$. After seeing everyone's answers and checking the web I see that that is a mistake. – Algebra 8 Jul 08 '18 at 16:57
  • You mean the answer which I have is wrong? – Key Flex Jul 08 '18 at 17:01
0

Using

Why it's true? $\arcsin(x) +\arccos(x) = \frac{\pi}{2}$

$$\operatorname{arccos} \frac{2}{\sqrt5} + \operatorname{arccos} \frac{3}{\sqrt{10}}=\pi-\left(\arcsin\dfrac2{\sqrt5}+\arcsin\frac{3}{\sqrt{10}}\right)$$

Now using Proof for the formula of sum of arcsine functions $ \arcsin x + \arcsin y $

as $$\left(\frac{2}{\sqrt5}\right)^2+\left(\frac{3}{\sqrt{10}}\right)^2=\dfrac45+\dfrac9{10}>1$$

$$\arcsin\dfrac2{\sqrt5}+\arcsin\frac{3}{\sqrt{10}}=\pi-\arcsin\left(\dfrac2{\sqrt5}\dfrac1{\sqrt{10}}+\dfrac1{\sqrt5}\dfrac3{\sqrt{10}}\right)=\pi-\arcsin\dfrac1{\sqrt2}=?$$

lab bhattacharjee
  • 274,582