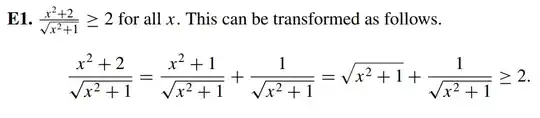Prove $\sqrt{x^2+1} + \frac{1}{\sqrt{x^2 +1}}\geq 2$

Question

I want to show why the last inequality in the problem below $\sqrt{x^2+1} + \frac{1}{\sqrt{x^2 +1}}\geq 2$ holds. It's clear that $x^2\geq 0$ and that equality holds when $x=0$ but how can I clearly show this. The left hand side, for $x^2>0$ is greater than $1$ but the right hand side becomes less than $1$ as $x^2>0$

By AM-GM $;\displaystyle \frac{;a + \dfrac{1}{a};}{2} \ge \sqrt{a \cdot \frac{1}{a}} = 1,$, then use it for $,a=\sqrt{x^2+1},$. — dxiv, Jul 30 '18 at 06:51
Also: Proving an inequality involving square roots and polynomials $\frac{a^2+2}{\sqrt{a^2+1}}\ge2$. — Martin R, Jul 30 '18 at 08:10

score 3 · Accepted Answer · answered Jul 30 '18 at 06:43

3

The inequality $(y-1)^{2} \geq 0$ gives $y+\frac 1 y \geq 2$ for any positive number $y$. Take $y=\sqrt {1+x^{2}}$.

answered Jul 30 '18 at 06:43

Kavi Rama Murthy

311,013

score 2 · Answer 2 · answered Jul 30 '18 at 06:43

2

The derivative of $f(y)=y+1/y$ is $1-1/y^2$, so the function $f$ increases in $[1,\infty)$, hence $f(y)\geq f(1)=2$.

answered Jul 30 '18 at 06:43

uniquesolution

18,541

f increases in [1,∞),And also decreases on $[0,1]$ which is needed to complete the argument. – dxiv Jul 30 '18 at 06:45
1

@dxiv - Since $\sqrt{x^2+1}\geq 1$ for all $x\in\mathbb{R}$, the interval $[0,1]$ is irrelevant. – uniquesolution Jul 30 '18 at 06:51
Right, but that belongs in the answer, not a comment. – dxiv Jul 30 '18 at 06:53
1

Feel free to include this in your answer. – uniquesolution Jul 30 '18 at 06:53
I didn't post an answer. Feel free to spell it out in your answer. – dxiv Jul 30 '18 at 06:54

Prove $\sqrt{x^2+1} + \frac{1}{\sqrt{x^2 +1}}\geq 2$

2 Answers2