The following relationships answer the question and do not need much explanation, just make the replacements to find the relevant limits. These are quite close approaches to the values of the roots x and y.
$y^4+By^3+Gy^2+Dy+E=0, \{B,G,D,E \} \in \mathbb{R}$
$c=G-3B^2/8$
$d=D+(B^3-4BG)/8$
$e=E-3B^4/256+(GB^2-4BD)/16$
$x^4+cx^2+dx+e=0$
$R=\sqrt{\frac{d^2}{4e}-c}$
$r=\sqrt{- \frac{d^2}{4e}-c}$
$p=\sqrt{\frac{d^2}{4|e|}-c}$
$x \in \mathbb{R}, e>0 \Rightarrow |x| \leq R$
$x \in \mathbb{R}, e<0 \Rightarrow |x| \leq r \sqrt{27/34}$
$x \in \mathbb{C} \Rightarrow |\Re (x)| \leq p$
$y \in \mathbb{R}, e>0 \Rightarrow -B/4-R \leq |y| \leq -B/4+R$
$y \in \mathbb{R}, e<0 \Rightarrow -B/4-r \sqrt{27/34} \leq |y| \leq -B/4+r \sqrt{27/34}$
$y \in \mathbb{C} \Rightarrow -B/4-p \leq | \Re (y)| \leq -B/4+p$
The above relations are based on the geometric interpretation of the quartic equation. I quote two relevant images:
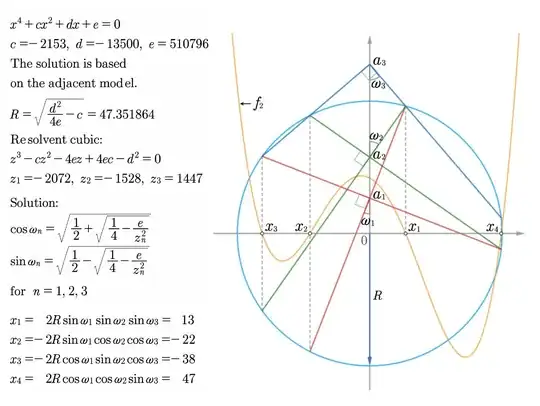
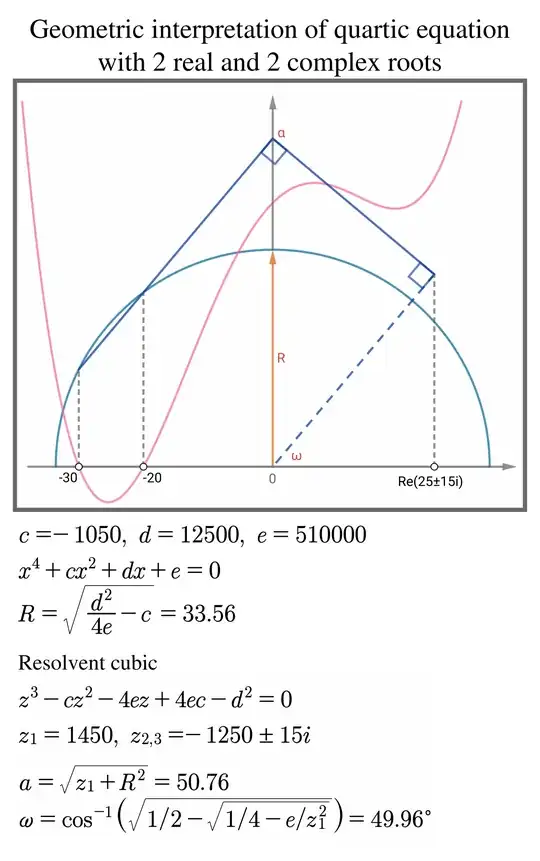
I add some details. To solve an equation of the form
$f(y)=y^4+By^3+Gy^2+Dy+E=0$
we first convert it to the form
$f(y-B/4)=(y-B/4)^4+B(y-B/4)^3+G(y-B/4)^2+D(y-B/4)+E$
$=x^4+cx^2+dx+e=0$
where the term $bx^3$ is absent because
$-b=x_1 + x_2 + x_3 + x_4 = 0$
From a geometric point of view, the graphs of the functions $f(y)$ and $f(y-B/4)$ are exactly the same, with the difference that the second of them has been moved parallel to the x-axis and has been installed at the beginning of the axes.

