Given that $\cos\frac{\pi}7, \cos\frac{3\pi}7 \cos\frac{5\pi}7$ are the roots of the equation $8x^3-4 x^2 - 4x + 1=0$ . The value of $\sin\frac{\pi}{14} ;\sin\frac{3\pi}{14} ;\sin\frac{5\pi}{14}$
1. I was trying to solve this problem using theory of equations taking the product of the roots to be $-1$.
Hint:
$$\dfrac\pi2-\dfrac{(2k+1)\pi}7=?$$ $k=0,1,2$
take $w = e^{k \pi i / 14}$ for any of $k = 1,3,5.$ Any satisfies $w^{14}+ 1 = 0.$ More precisely, $w \neq i$ and $$ w^{12} - w^{10} + w^8 - w^6 + w^4 - w^2 + 1 = 0. $$
Then $2 \sin \frac{k \pi}{14} = \frac{w - \frac{1}{w}}{i} = \frac{w^2 - 1}{i w};$ let us name
$$ x = \frac{w^2 - 1}{i w}. $$
A little fiddling shows
$$ -x^6 + 5 x^4 - 6 x^2 + 1 = \frac{w^{12} - w^{10} + w^8 - w^6 + w^4 - w^2 + 1}{w^6} $$ which is actually $0.$ Our double sines are roots of $x^6 - 5 x^4 + 6 x^2 - 1.$ Taking $x=2s$ tells us that the original sines (as well as their negatives) are roots of
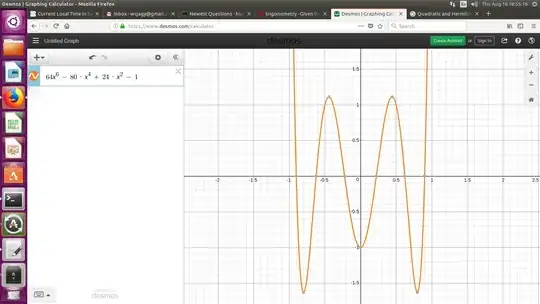
$$ 64s^6 - 80 s^4 + 24 s^2 - 1 $$
