29

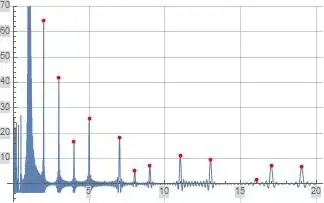
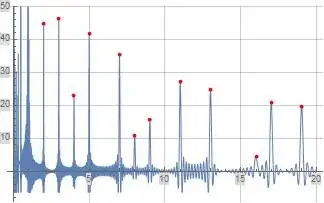
On the one hand, the Prime Counting Function $\pi_0(x)$ maybe be written $$ \pi_0(x) = \operatorname{R}(x^1) - \sum_{\rho}\operatorname{R}(x^{\rho}) \tag{1} $$ with $ \operatorname{R}(z) = \sum_{n=1}^{\infty} \frac{ \mu (n)}{n} \operatorname{li}(z^{1/n})$ and $\rho$ running over all the zeros of $\zeta$ function. The derivative of $(1)$ is $$ \pi_0'(x) = \operatorname{R}'(x) - \sum_{\rho}\operatorname{R}'(x^{\rho}) \tag{2} $$ with $\displaystyle \operatorname{R}'(x^k) = \sum_{n=1}^{\infty} \frac{ \mu (n)}{n} \frac{x^{k/n-1}}{\log x}$.

On the other hand, we have $$ \pi_1(x)=\sum_{k=1}^{\infty} H(x-p_k), $$ with $H(\cdot)$ being the Heaviside function. This would result in (a prime comb) $$ \pi_1'(x)=\sum_{k=1}^\infty \delta(x-p_k).\tag{3} $$

$(3)$ obviously diverges at a prime $p_k$. Is it possible to show that $(2)$ also diverges?

Thanks to Raymond there is also a nice gif:

$\hskip1.7in$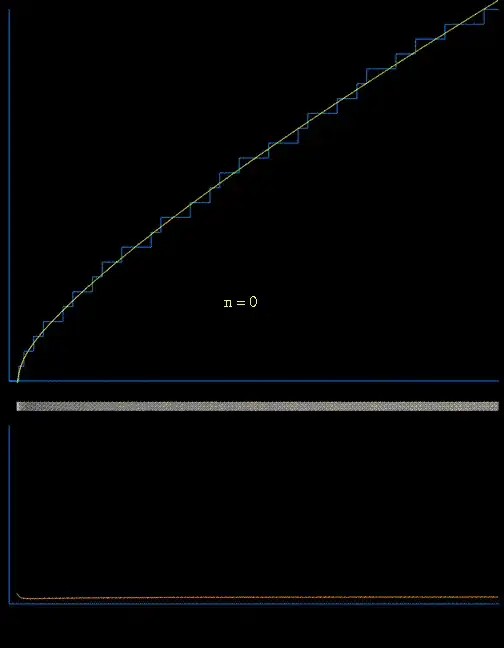what text

The lower animated graph is the derivative of the function above, and we see the positions of the primes emerging as Dirac delta-type spikes. The horizontal bar in the middle has been constructed so that the intensity of brightness is related to the absolute value of the derivative. In this way we see the positions of the primes gradually emerge as narrow bands of light. [for reference see Matthew Watkins homepage].

Community
  • 1
draks ...
  • 18,449
  • 3
    Even deriving (2) from (1) requires an assumption - namely that the sequence of partial sums in (2) converges uniformly to the full series - and I don't think that holds here. (The same proviso holds for your expression for $R'$, though there the convergence might well be uniform.) See http://en.wikipedia.org/wiki/Uniform_convergence#To_differentiability – Greg Martin Dec 26 '13 at 19:19
  • The series in (1) is an asymptotic series, it doesn't converge in the usual sense. I don't think that it has even been established in what sense one can take the equality there literally. – Count Iblis Jun 20 '18 at 14:08
  • @CountIblis ok, but the gif Raymond provided, looks intriguingly. Why do Dirac delta-type spikes emerge when you just do it? Would it help to further characterise the what of type of spikes emerge? Not necessarily delta-type ones... – draks ... Jun 21 '18 at 06:05

1 Answers1

2

Since your formula (1) has never been proven to converge (see Weisstein, Eric W. "Riemann Prime Counting Function." From MathWorld--A Wolfram Web Resource), you might be better off looking at $\Pi'(x)$ and/or $\psi'(x)$ defined in (1) and (2) below with explicit formulas defined in (3) and (4) below. Note $\psi_o'(x)=\log(x)\,\Pi_o'(x)$.

(1) $\quad\Pi'(x)=\sum\limits_{n=2}^\infty\frac{\Lambda(n)}{\log(n)}\,\delta(x-n)\quad\text{(derivative of Riemann's prime-power counting function)}$

(2) $\quad\psi'(x)=\sum\limits_{n=1}^\infty\Lambda(n)\,\delta(x-n)\quad\text{(derivative of second Chebyshev function)}$

(3) $\quad\Pi_o'(x)=\frac{1}{\log(x)}\left(1-\sum\limits_\rho x^{\rho-1}-\sum\limits_{n=1}^\infty x^{-2\,n-1}\right)=\frac{1}{\log(x)}\left(1-\sum\limits_\rho x^{\rho-1}-\frac{1}{x\,\left(x^2-1\right)}\right)$

(4) $\quad\psi_o'(x)=1-\sum\limits_\rho x^{\rho-1}-\sum\limits_{n=1}^\infty x^{-2\,n-1}=1-\sum\limits_\rho x^{\rho-1}-\frac{1}{x\,\left(x^2-1\right)}$

The following two figures illustrate formulas (3) and (4) defined above for $\Pi_o'(x)$ and $\psi_o'(x)$ respectively where both formulas are evaluated over the first $200$ pairs of non-trivial zeta zero. The red discrete portions of the two figures below illustrate the evaluation of formulas (3) and (4) at prime-powers.

Illustration of Formula (3)

Figure (1): Illustration of Formula (3) for $\Pi_o'(x)$

Illustration of Formula (4)

Figure (2): Illustration of Formula (4) for $\psi_o'(x)$

Steven Clark
  • 7,363