The line HC is a median in triangle $\triangle BCE$
How would I prove that for two arbitrary sized squares any angle $\alpha$, $\angle DIC$ is 90 degrees?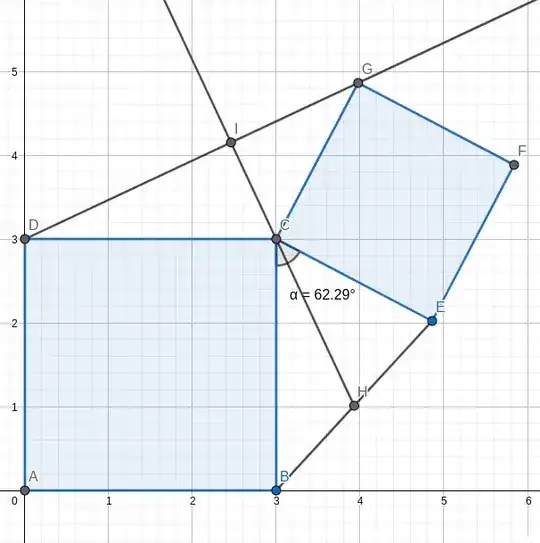
I have tried playing around with this in geogebra but to no avail.
The line HC is a median in triangle $\triangle BCE$
How would I prove that for two arbitrary sized squares any angle $\alpha$, $\angle DIC$ is 90 degrees?
I have tried playing around with this in geogebra but to no avail.
Choose point $J$ on line $BC$ such that $BC=CJ$. Let us focus on (green) triangle $DCG$ and (red) triangle $JCE$.
$$\angle DCG = \angle JCE = \angle JCG + 90^\circ$$
$$DC=JC,\space CG=CE$$
By SUS, triangles $DCG$ and $JCE$ are congruent and therefore $JE=DG$ and $\angle CDG = \angle CJE$. But $CD\bot CJ$ so it must be that:
$$JE\bot DG$$
(This is also obvious form the fact that triangle $JCE$ can be obtained by rotating triangle $DCG$ for $90^\circ$).
$C$ is the midpoint of $BJ$ and $H$ is the midpoint of $BE$. So lines $CH$ and $JE$ must be parallel. $JE$ is perpendicular to $DG$ and therefore $CH$ must be perpendicular too.
This also proves an interesting fact that $DG=2CH$