Ok so I was playing with GeoGebra by plotting various functions, then I come up with the following kind of graph when I plot $\log(x)$ to various positive powers and $f(x)=x$.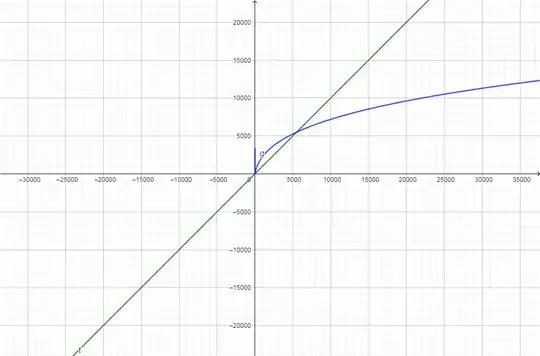 
The green one is the function $f(x)=x$ and the blue one is $g(x)=(\log(x))^4$. So it seems for sufficiently large $x$, any positive power of $\log(x)$ is less than $x$. But I am unable to prove this fact. Can anyone give me a hint as how to approach to this problem?
Clearly this is true iff $x < e^{x^{1/p}}$ for sufficiently large x (or $x^p < e^x)$.
What if we proved that for sufficiently large $x$, $m$, $(1+ 1/m)^{mx} > x^p$? Also, derivatives have some interesting properties.
We have $$\log^p(x)<x\iff\log(x)<x^{1/p}\iff\frac{\log(x)}{x^{1/p}}<1$$
Taking the limit to check the behaviour when $x$ is large: $$\lim_{x\to\infty}\frac{\log(x)}{x^{1/p}}=\lim_{x\to\infty}\frac{\frac{d}{dx}\log(x)}{\frac{d}{dx}x^{1/p}}=\lim_{x\to\infty}\frac{1/x}{x^{1/p-1}/p}\\=\lim_{x\to\infty}\frac{p}{x^{1/p}}=0<1$$
So for sufficiently large $x$ we have $\log^p(x)<x$
To prove that $0=\lim_{x\to \infty}(\log x)^Ax^{-B}$ for any $A,B>0$ by elementary means, first observe that $$0=\lim_{x\to \infty}(\log x)^Ax^{-B}\iff$$ $$\iff 0=\lim_{x\to \infty}((\log x)x^{-B/A})^A\iff$$ $$\iff 0=\lim_{x\to \infty} (\log x)x^{-B/A} .$$ For brevity let $y=(B\log x)/A.$ Let $[y]$ denote the largest integer not exceeding $y.$ If $x>e^{2A/B}$ then $y\geq [y]\geq 2.$ So by the Binomial Theorem, if $x>e^{2A/B}$ then $$x^{B/A}=e^y>2^y\geq 2^{[y]}=\sum_{j=0}^{[y]}\binom {[y]}{j}>$$ $$> \binom {[y]}{2}=[y]([y]-1)/2>$$ $$>([y]-1)^2/2>(y-2)^2/2.$$ Now $x>e^{2A/B}$ also implies $x^{B/A}>2$. Therefore if $x>e^{2A/B}$ then $$(A/B)\sqrt {3x^{B/A}}\;>(A/B) \sqrt {2x^{B/A}+2}\;>$$ $$>(A/B)y=\log x$$ and hence $(A/B)(\sqrt 3\;) x^{-B/2A}>(\log x)x^{-B/A}>0.$ So $\lim_{x\to \infty}(\log x)x^{-B/A}=0.$
Note that, with the substitution $t=x^{1/p}$, $$ \lim_{x\to\infty}\frac{x^{1/p}}{\log x}= \lim_{t\to\infty}\frac{t}{p\log t}=\infty $$ with a very simple application of l'Hôpital.
