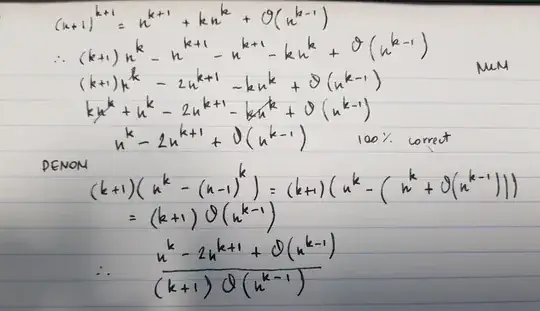This question is linked to my previous question since I am not able to spot my error.
Let $\tilde{x}_n = (k+1)(1^k + ... + n^k) - n^{k+1}$, $\tilde{x}_{n-1} = (k+1)(1^k + ... + (n-1)^k) - (n-1)^{k+1}$. Then, $\tilde{x}_n - \tilde{x}_{n-1} = (k+1)n^k - n^{k+1} + (n-1)^{k+1}$. And the denominator will be $(k+1)(n^k - (n-1)^k)$. Therefore, need to find limit of
$$\lim_{n \to \infty} \frac{(k+1)n^k - n^{k+1} - (n+1)^{k+1}}{(k+1)(n^k - (n-1)^k)}$$
Here is my solution: