$\left|\sin(x)\right|$ derivative at $\pi$

Question

Let $f$ be a function, $f:\mathbb{R}\to\mathbb{R}$

$$f(x)=\begin{cases} e^{x^2}-2 & x< 0 \\ x^3+x-1 & 0\leq x \leq 1 \\ \left|\sin(x)\right| & x>1. \end{cases}$$

Check if $f$ is continuous and differentiable at $a$, when $a=0,1,\frac{\pi}{2}, \pi$. If $f$ is differentiable at $a$, find $f'(a)$.

What I've been doing:

I found that:

• $f$ is continuous at $0$ but not differentiable.
• $f$ is not continuous at $1$ so it's not differentiable.

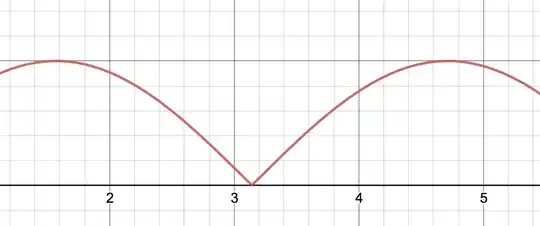
And then I thought that $f$ was differentiable at $\pi$ and $\frac{\pi}{2}$ because $f$ is continuous at $(1, +\infty)$ ($\left|\sin(x)\right|$), so I looked for:

1. $f'(\frac{\pi}{2})=\left|\cos(\frac{\pi}{2})\right|=0$ (by the solution my prof gave me this is correct).
2. $f'(\pi)=\left|\cos(\pi)\right|=-1$ Now this is wrong. The solution they gave me says that $f$ is not differentiable at $\pi$, and I'm really lost. Why is it differentiable at $\frac{\pi}{2}$ and not $\pi$?

Answer 1

• $f$ behaves like $\sin(x)$ around $\frac{\pi}{2}$. It is differentiable.

• $f$ behaves like $\sin(x)$ on the left of $\pi$ but it behaves like $-\sin(x)$ on the right. We have to be more careful.

• $f(\pi)=0$.

• $\lim_{x \to \pi^-} \frac{f(x)-f(\pi)}{x-\pi}=\lim_{x \to \pi^-} \frac{f(x)-0}{x-\pi}=\lim_{x \to \pi^-} \frac{\sin(x)-\sin(\pi)}{x-\pi}=\cos(\pi)=-1$

• $\lim_{x \to \pi^+} \frac{f(x)-f(\pi)}{x-\pi}=\lim_{x \to \pi^+} \frac{-\sin x-0}{x-\pi}=-\lim_{x \to \pi^+} \frac{\sin(x)}{x-\pi}=-\lim_{x \to \pi^+} \frac{\sin(x)-\sin(\pi)}{x-\pi}=-\cos(\pi)=1$

Hopefully this picture can help you, notice where the kink occurs.

Answer 2

Intuitively, $|\sin x|$ is not differentiable at $x=\pi$ because the graph comes to a sharp corner there.

To make this reasoning rigorous, set $f(x)=|\sin x|$ and look at the difference quotient

$$\frac{f(\pi+h)-f(\pi)}{h}=\frac{|\sin(\pi+h)|}{h}$$

When $h\to0^{+}$, the difference quotient is $-\frac{1}{h}\sin(\pi+h)=\frac{1}{h}(\sin h)$, which tends to $1$.

But when $h\to0^{-}$, the difference quotient is $\frac{1}{h}\sin(\pi+h)=-\frac{1}{h}(\sin h)$, which tends to $-1$.

Therefore the two-sided limit of the difference quotient as $h\to 0$ does not exist.

So $f$ is not differentiable at $x=\pi$.

---

Note that my answer does not look at the limit of $f'$. It looks at the limit of the difference quotient, working directly from the definition of the derivative.

Answer 3

hint:

A derivative is defined by a limit: $$ f'(x)=\lim_{h\rightarrow 0} \frac{f(x+h)-f(x)}{h} $$

As any limit, you must check that this limit does not depend on the path you use to compute it

In $\mathbb{R}$, only two paths are possibles: coming from the left or coming from the right, hence to prove derivability at $x$ you must check that $$ \lim_{h\rightarrow0_+} \frac{f(x+h)-f(x)}{h} = \lim_{h\rightarrow 0_-} \frac{f(x+h)-f(x)}{h} $$

Answer 4

$f$ is indeed discontinuous at $x=1$.

Then from the function definition,

$$f'(x)=\begin{cases} 2xe^{x^2} & x< 0 \\ 3x^2+1 & 0<x <1 \\ \cos(x) & 1<x<\pi \\-\cos(x) & \pi<x. \end{cases}$$

We have mismatches between derivatives on the left and on the right at $x=0$ and $x=\pi$.

Answer 5

Note that in the interval $[1, \pi]$, we have $f(x) = |\sin(x)| = \sin(x)$ because $\sin(x) \geq 0$. However, for $x \in [\pi, 2 \pi]$, we have $f(x) = -\sin(x)$ because $\sin(x) \leq 0$. Therefore, $$ \lim_{x \to \pi^{-}} f'(x) = \lim_{x \to \pi{-}} \cos(x) = -1$$ and $$ \lim_{x \to \pi^{+}} f'(x) = \lim_{x \to \pi^{+}} (-\cos(x)) = 1$$ Hence, $f$ is not differentiable at $x = \pi$.

Answer 6

Let's look at how to derivative behaves near $\pi$. To make things simple, we can regard the function as $sin(x)$ at the left neighborhood of $\pi$ and as $-sin(x)$ at the right neighborhood of $\pi$ (and as $0$ at $x=\pi$).

This means that the derivative on the left side of the point is $cos(x)$ and on the right side of the point is $-cos(x)$. As $x$ approaches $\pi$ from the left, the derivative approaches $cos(\pi)=-1$. As $x$ approaches $\pi$ from the right, the derivative approaches $-cos(\pi)$=1. This is a contradiction to Darboux's theorem (can you explain why?), therefore the derivative does not exists at $x=\pi$.

You can also show this directly using the definition of the derivative, but I believe this explanation is sufficient.

Answer 7

Be carefull with absolute values. You have the function $\sin(x)$ changing sign at $\pi$, so its absolute value can have a "sharp" non-differentiable point at $\pi$. That is what is happening.

You have $$|sin(x)|=\left\{ \begin{array}{c} \sin(x)\text{, for }x\leq\pi \\ -\sin(x)\text{, for }x\geq\pi \end{array}\right. $$

That means that in a neighbourhood of $\pi$ it is $\frac{d|sin(x)|}{dx}\neq|cos(x)|=cos(x)$, but rather $$\frac{d|sin(x)|}{dx}= \left\{\begin{array}{c} \cos(x)\text{, for }x\leq\pi \\ -\cos(x)\text{, for }x\geq\pi \end{array}\right.$$ wich is not continuous at $\pi$