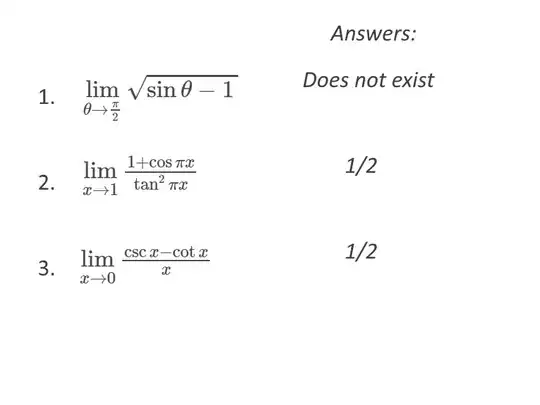0

Problems with corresponding solutions

I don't understand why #1 is "does not exist" as opposed to 0. I also don't know how to begin solving #2 and #3. When I look it up, the only solutions involve L'Hopital's Rule but my teacher hasn't taught us it yet so I can't use it. Any help is appreciated!

user604369
  • 45
  • 1
    For #1, you should clarify whether you are looking at specifically real number sequences or if you are looking at complex number sequences. For all real numbers $\theta$ in a small enough neighborhood of $\pi/2$ you have $\sin \theta - 1$ is negative and the square root of a negative number is nonreal, hence DNE. If you were looking at complex sequences, I agree it looks like it should converge to zero. – JMoravitz Oct 18 '18 at 00:22

2 Answers2

1

For the first one the expression under the radical sign is negative for $\theta \ne \pi/2 $ so it is not real.

For the second one multiply top and bottom by $1-\cos \pi x$ and turn the top into $\sin^2 \pi x$

Then write the $\tan ^2 \pi x$of the bottom in terms of $ \sin \pi x$ and $\cos \pi x$ and cancel the $\sin ^2 \pi x$ from top and bottom.

The rest is easy.

The third one is similar to the second one.

Mohammad Riazi-Kermani
  • 68,728
0

for the second and third use:

$$ \frac1{\tan^2 \pi x} = \frac{\cos^2 \pi x}{(1+\cos \pi x)(1-\cos \pi x)} $$

and

$$ \csc x - \cot x = \frac{1-\cos x}{\sin x} = \frac{2 \sin^2 \frac{x}2}{2\sin \frac{x}2 \cos \frac{x}2} $$

respectively

David Holden
  • 18,040