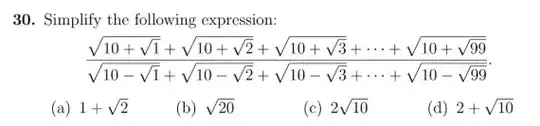I can't seem to find a way, squaring the expression would make more terms and would make it harder, I guess there must be something to do with the first and last terms as they sum to 100? or maybe difference of to squares, but i can't solve it.
-
Interesting. Crude estimates quickly tell you which of those answers is correct (all but one are too large). And a quick numerical calculation confirms the result, but I don't see a cheap algebraic mode of attack. – lulu Oct 18 '18 at 15:22
-
5Numerical computation strongly supports the conjecture that $$\sum_{k=1}^{n^2-1}\sqrt{n+\sqrt{k}}=(1+\sqrt2)\sum_{k=1}^{n^2-1}\sqrt{n-\sqrt{k}}$$ for $n\geq2$ I don't have any idea how to attack it yet. – saulspatz Oct 18 '18 at 16:04
-
What is the source of this problem? – saulspatz Oct 18 '18 at 16:38
1 Answers
Useful fact:
$$ \sqrt{a\pm \sqrt{b}}= \sqrt{\frac{a+\sqrt{a^2-b}}{2}} \pm \sqrt{\frac{a-\sqrt{a^2-b}}{2}} \tag{1}$$
Proof:
\begin{align} RHS^2 &= \frac{a+\sqrt{a^2-b}}{2}+\frac{a-\sqrt{a^2-b}}{2} \pm 2 \sqrt{\left( \frac{a+\sqrt{a^2-b}}{2} \right) \left( \frac{a-\sqrt{a^2-b}}{2} \right)} \\ &= a \pm 2\sqrt{\frac{a^2-(a^2-b)}{4}} \\ &= a \pm 2\sqrt{\frac{b}{4}} \\ &= a \pm \sqrt{b} \\ &= LHS^2 \\ LHS &= RHS \qquad (a^2 \ge b \ge 0) \end{align}
Let
$$S_{\pm}=\sum_{j=1}^{n^2-1} \sqrt{n \pm \sqrt{j}} \tag{2}$$
and reverse the order of summation by taking $\, k=n^2-j$, then
$$S_{\pm}=\sum_{k=1}^{n^2-1} \sqrt{n \pm \sqrt{n^2-k}} \tag{3}$$
Now by $(1)$, $(2)$ and $(3)$,
$$S_{\pm}=\frac{S_+ \pm S_-}{\sqrt{2}} \implies \frac{S_+}{S_-}=1+\sqrt{2}$$
- 18,990
-
2
-
-
@Supermage1 Well that could be easy. Just form perfect squares inside the radicals. So just solve $xy=b/4$ and $x+y=a$ to get $x, y$ ans hence the the original radical would equal $\sqrt x+\sqrt y$ – Rohan Shinde Oct 19 '18 at 02:26
-
@SuperMage1 I've added a proof for the identity $(1)$ in my answer. And what Manthanein suggested is to find $x$ and $y$ such that $LHS=\sqrt{x+y \pm 2\sqrt{xy} ,}=|\sqrt{x} \pm \sqrt{y} ,|$. – Ng Chung Tak Oct 19 '18 at 09:13