Arithmetic mean is at least as large as the geometric mean: $\frac{(s_1+...+s_n)}{n}\geq(s_1 \cdot ...\cdot s_n)^{1/n}$

Question

Let $s_n\in\mathbb{R}_{\geq0}$ for all $n\in\mathbb{N}.$ $$\frac{(s_1+...+s_n)}{n} \geq (s_1 \cdot ...\cdot s_n)^{1/n}$$

How do I prove this inequality? I'm able to prove it for $n=2$. Do I need to do this with induction? Any hint ?

Answer 1

This is what is known as the Arithmetic Mean-Geometric Mean inequality, or AM-GM for short. There are a number of proofs for this, some of them quite clever. I will describe that which I find the most clever. The "standard" proof lies in a leap forward-fall back type of induction by Cauchy. George Polya has claimed that this proof came to him in a dream, and that it was "the best mathematics he had ever dreamt". It starts with noticing that $$1+x\le e^x$$ which is justifiable in a number of ways, including the following graph:

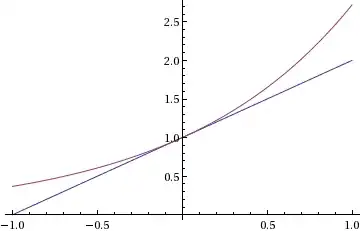
Changing variables $x \mapsto x-1$ gives the inequality $x \le e^{x-1}$, and applying this to a finite set of real numbers $\{s_k\}$ and exponents $p_k$ such that their sum is $1$ we get: $$s_k^{p_k}\le e^{p_ks_k-p_k}$$ And multiplying them all together, getting a weighted geometric mean, gives the following inequality $$s_1^{p_1}s_2^{p_2}\dots s_n^{p_n} \le \exp\left(\sum_{k=1}^np_ks_k -1\right)$$ At this point you might notice that the term in the exponential is just the arithmetic mean, $AM$, but noticing also that we still have $AM \le e^{AM-1}$ we seem to have shown nothing more than that there exists an upper bound for both of the quantities we are comparing. This seems rather counterintuitive, but it does give a comparison between $AM $ and $GM$. We just need to apply this inequality with $$s'_k = \frac{s_k}{AM}$$ Which gives $$\prod_{k=1}^{n}\left(\frac{s_k}{AM}\right)^{p_k}\le\exp\left(\sum_{k=1}^np_k\frac{s_k}{AM} -1\right) =\exp(1-1) = 1$$ But remembering that the sum of the $p_k$ is equal to 1 as they are weights, so multiplying both sides by $AM$ gives $$GM\le AM$$ for any arbitrary weights, and your question follows a forteriori with $p_k = \frac{1}{n}$.

Answer 2

A simpler proof can be derived by using $\ln(x)$ instead. Note that it's a concave and increasing function. Let $\Sigma p_i=1, p_i \ge 0$
$$\ln(\Sigma p_i s_i) \ge \Sigma p_i \ln s_i = \Sigma \ln {s_i}^{p_i} = \ln \Pi {s_i}^{p_i}$$ Therefore $$\Sigma p_i s_i \ge \Pi {s_i}^{p_i}$$ Setting $p_i = \frac1n$ gives you AM $\ge$ GM.