1

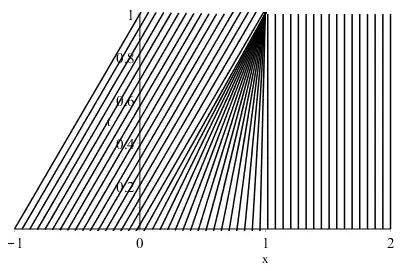
Burgers Equation

Consider the initial value problem for Burgers' equation

$$ \begin{align}\begin{cases} u_{t} + u u_{x} = 0 \\ u(x,0) = \phi(x) \end{cases} \end{align} \tag{1}$$

our initial data is given as

$$ \phi(x)= \begin{align}\begin{cases} 1 & x \leq0 \\ 1 -x & 0 < x < 1 \\ 0 & x \geq 1 \end{cases} \end{align} \tag{2}$$

The characteristics are then given by

$$ \frac{dx}{dt} = u \\ \frac{du}{dt} =0 \tag{3} $$

When we solve them we should get

$$ x(t) = ut +x_{0} \tag{4} $$

$$ u(t) = c_{0} $$

then we get

$$ u = c_{0} = \phi(x_{0}) \tag{5} $$

$$ x(t)= \phi(x_{0})t + x_{0} \tag{6} $$

so our solution is given by

$$ u(x,t) = \phi(x_{0}) = \phi(x-ut) \tag{6} $$

$$ u(x,t) = \begin{align}\begin{cases} 1-c_{0}t & x \leq0 \\ 1 -x+c_{0}t & 0 < x < 1 \\ -c_{0}t & x \geq 1 \end{cases} \end{align} \tag{7}$$

So then if we have $u(x,0) =\phi(x-u\cdot 0)$ = $\phi(x)$ we would have

$$ u(x,0) = \begin{align}\begin{cases} 1 - c_{0} \cdot 0 & x \leq0 \\ 1 -x+c_{0}\cdot 0 & 0 < x < 1 \\ -c_{0} \cdot 0 & x \geq 1 \end{cases} \end{align} \tag{8}$$

which is

$$ \phi(x)= \begin{align}\begin{cases} 1 & x \leq0 \\ 1 -x & 0 < x < 1 \\ 0 & x \geq 1 \end{cases} \end{align} \tag{9}$$

EditPiAf
  • 20,898
  • 1
    (a) What's $x_0$? (b) If you have an explicit "solution", the easiest way to check if it is actually correct is to plug what you wrote into the original equation and see if the equality is satisfied. (c) The meaning of your equation (3) is a little bit unclear. Please explain a bit more. And if you explain how you get from (3) to (4), someone may be able to point out where the problem is. – Willie Wong Nov 06 '18 at 03:53
  • i have edited it. –  Nov 06 '18 at 04:20
  • Okay, now with your work shown: from where did you get the quantity "x_0 \cdot t"? In all of your previous lines you only have $c_0 t$ or $u t$. Where did the $x_0$ come from? – Willie Wong Nov 06 '18 at 04:26
  • ahhh...I think I was writing it before..using that constant. –  Nov 06 '18 at 04:29
  • 2
    More to the point: the method of characteristics should tell you that $$ u(x_0 + t \phi(x_0), t) = \phi(x_0)$$ Do you see where this comes from? Now, if $x = x_0 + t \phi(x_0)$, can you solve (using the explicit function $\phi$) for $x_0$ in terms of $x$ and $t$? – Willie Wong Nov 06 '18 at 04:29
  • 2
    (Hint: you may find this last step a bit difficult, for good reasons. If $x_0 = 0$ and $t = 1$, you find $x = 1$; but if $x_0 = 1$ and $t = 1$, you find also that $x = 1$. What does this mean?) – Willie Wong Nov 06 '18 at 04:32

1 Answers1

2

The method of characteristics gives the implicit equation $u = \phi(x-ut)$. Therefore, if $x-ut\leq 0$, we have $u=1$. If $x-ut\geq 1$, we have $u=0$. Otherwise, we have $u = \frac{1-x}{1-t}$. To summarize the solution obtained via the method of characteristics, $$ u(x,t) = \left\lbrace \begin{aligned} &1 && x\leq t\\ &\tfrac{1-x}{1-t} && t<x<1\\ &0 && 1\leq x \end{aligned} \right. $$ which is valid for $t<1$. At $t=1$ (breaking time), characteristics intersect and a shock wave occurs. This is illustrated on the following plot of the characteristic curves in the $x$-$t$ plane

characteristics

See this post for a book reference.

EditPiAf
  • 20,898