$e^{\sin(x)}-1$ has the same roots as $\sin(x)$. What is the difference between infinite product series expansions of $\sin(x)$ and $e^{\sin(x)}-1$ if they both have same infinite roots ?
Asked
Active
Viewed 156 times
9
-
2They may have the same roots, but effectively, sin(x) differs everywhere else in many ways from your function. Simple derivative analysis can show you that fact. They have different critical points, points of inflection, etc.. So, the series will be much different – KKZiomek Nov 17 '18 at 15:48
-
3I think that this Wikipedia article can give some insight about this... – rafa11111 Nov 17 '18 at 15:51
-
2If you mean the real variable $x$ then they differ by a function without zeros $\frac{e^{\sin x}-1}{\sin x}$ (compare with $p_1(x)=x-1$ and $p_2(x)=2x-2$). For complex $x$ the first function has more zeros, e.g. a solution to $\sin x=2\pi i$ is a zero of the first function that is not zero of the second one. – A.Γ. Nov 17 '18 at 15:54
-
Is there a factorization formula for it like https://math.stackexchange.com/questions/157372/proving-frac-sin-xx-left1-fracx2-pi2-right-left1-fracx22 ? – Omid Motahed Nov 17 '18 at 16:30
-
If $f(z)/g(z)$ is entire and has no zeros then $f(z) = g(z) e^{h(z)}$ with $h(z)$ entire. This is also the way to express any meromorphic function as a series over its poles and any entire function as a product over its zeros – reuns Nov 18 '18 at 02:50
-
Main reason I become interested was I read a book showing how Euler calculated sum of the inverse squares using infinite product series of sin(x) .Its Taylor expansion is simple https://www.wolframalpha.com/input/?i=expand+e%5Esin(x) – Omid Motahed Nov 18 '18 at 06:21
1 Answers
1
It is possible to consider an example of a non-zero multiple of a function. while they are not equal, they have the same zeros.
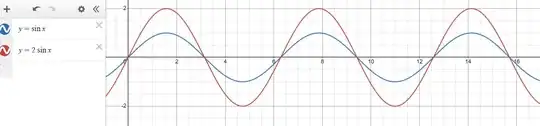Similarly, the following functions even though have identical infinite roots but aren't the same.
Therefore, we don't expect same power series expansion for such two functions.
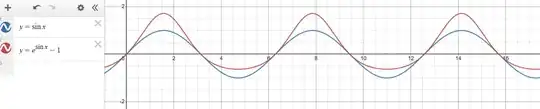
Henry
- 332